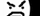First thing we do is choose a player name and banner (which doesn't mean shit)
After that, we read the briefing.
I hope you can read that. It might not have been the best idea to get blue text on the background of a blue farseer... It's easier on the eyes in the game itself because the briefings are voice-acted by Farseer Badass (the same one from the intro)
And our objectives. Basically, wipe everything off the map.
Time to manage our army...
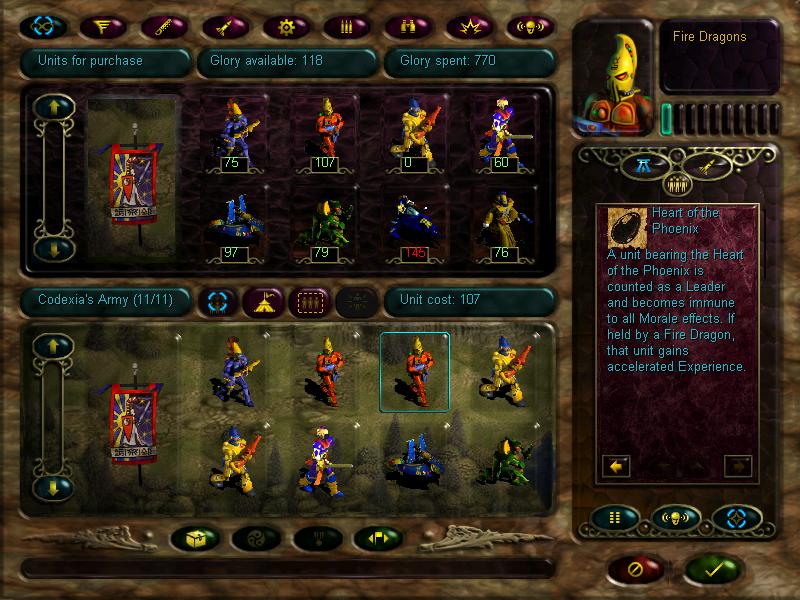
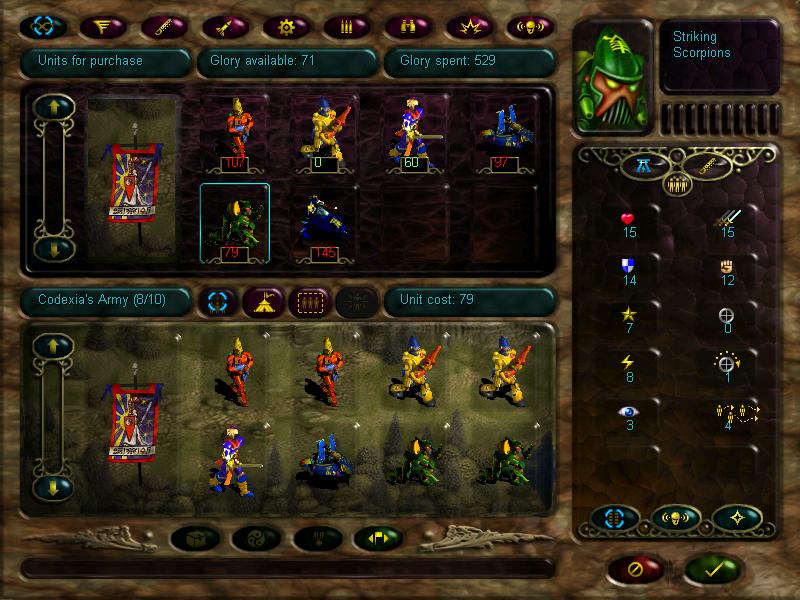
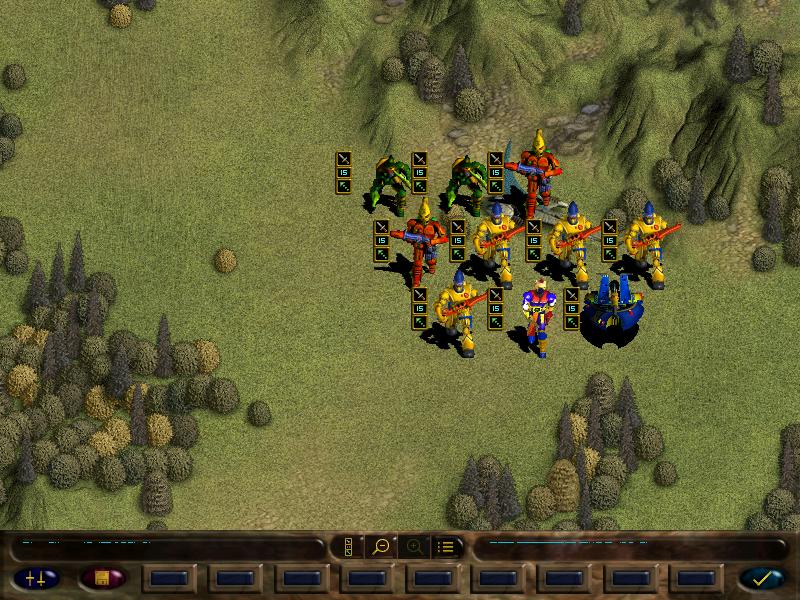
Here are the bros we can get for our strike team.
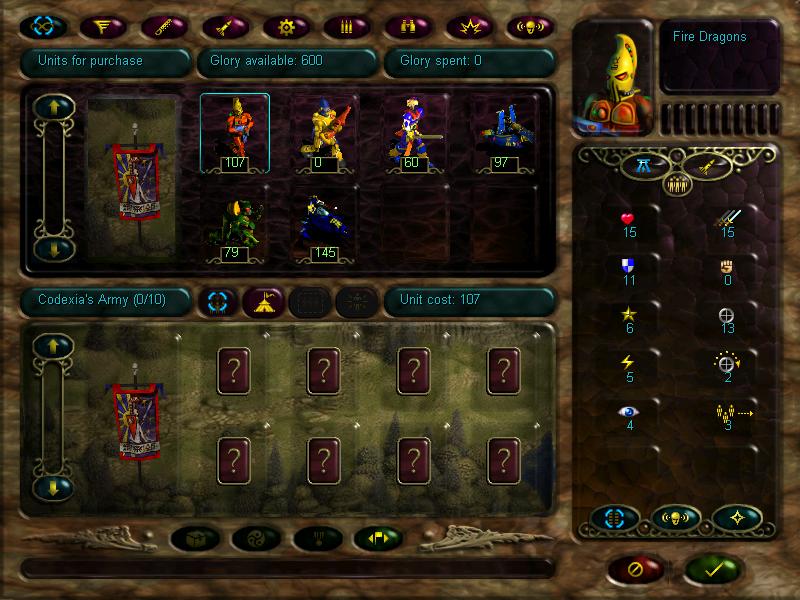
All units (and later upgrades for them) cost 'glory'. Glory is a resource replenished by completing missions and exploring key locations on the mission map. For the next mission, we can get only 10 units.
Here are the bros available to us:
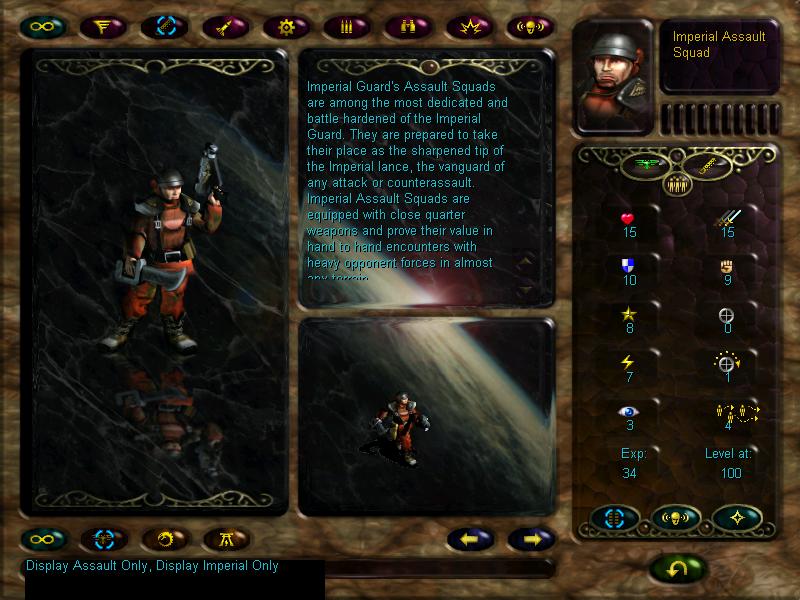
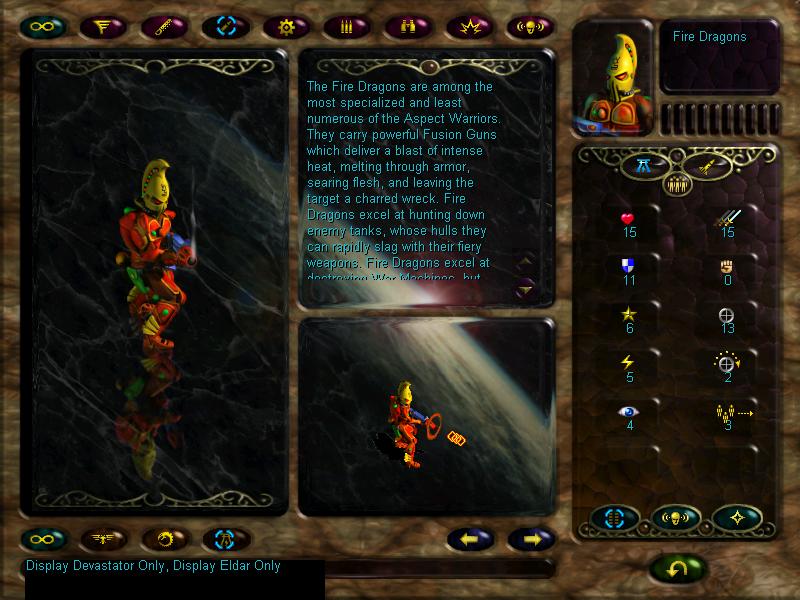
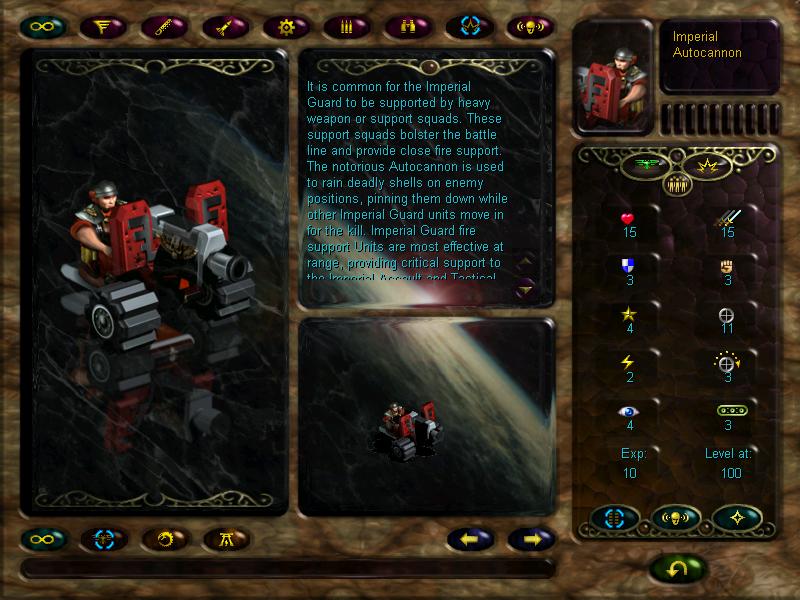
Fire dragons will be our sternguard. They have the 'armour piercing' ability, which makes them fry warmachines at an excellent rate. They are also of the 'devastator' class, which means they can launch support fire if in range of enemy units attacking friendly ones. But they should be kept in the back (at least later on), as their defence is a little lacking. They're also slow as shit which can bite you in the arse in timed missions.
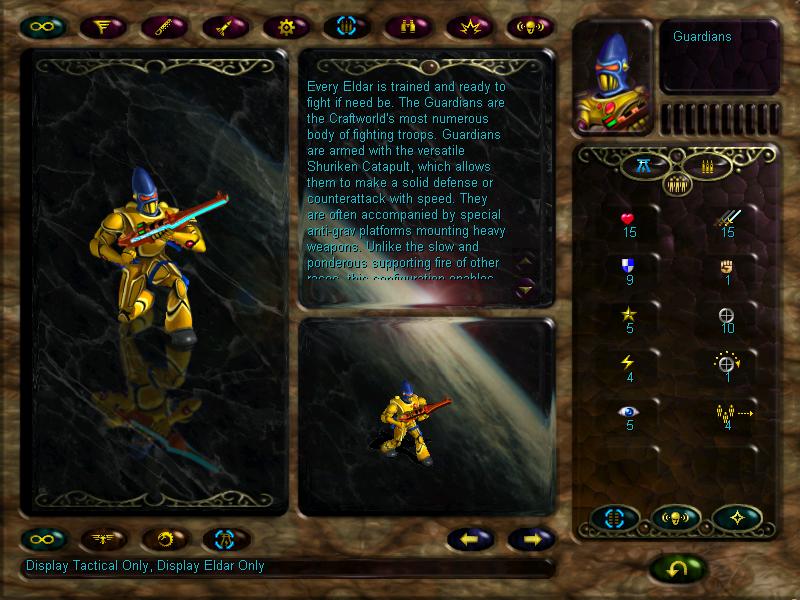
Next are the guardians. This will be our cannon fodder. Essentially, guardians are completely useless, and the worst unit available to us (that's why they cost 0 glory). But their big advantage is that they gain experience faster than other units, and at level 4 they can advance to aspect warriors.
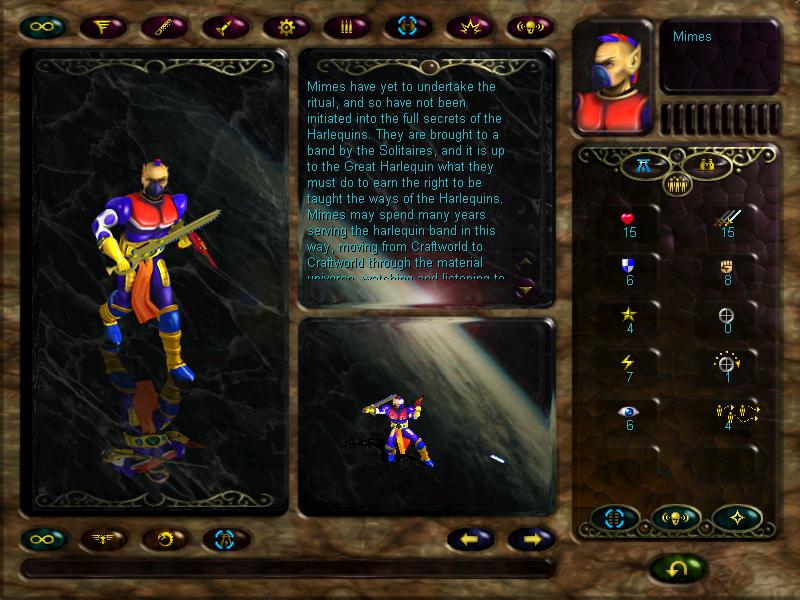
Mimes will be our early scouts. They have pretty good movement and visibility range, and later can upgrade to harlequins. They have two neat special abilities - invisibility, which makes them unseen to the enemy, and gives them the ability to strike without provoking an enemy counterattack. The second is 'hit and run', which allows them to move a few times during their turn, as opposed to other units that can't move anymore if they advance by one hex, even if their mobility is 5. However, caution is advised when using them, as their defence is pitiful.
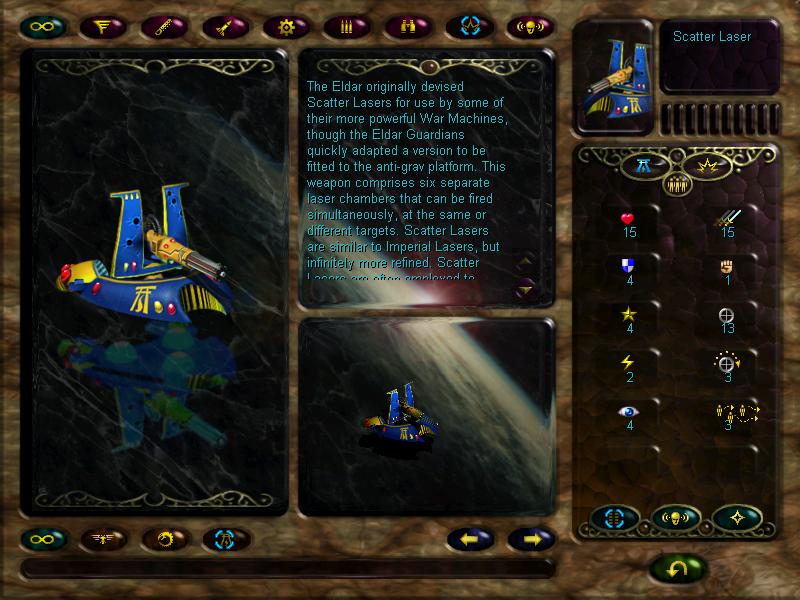
Very early artillery, the scatter laser might die fast, but it's extremely useful if used well. It has a long range (3), a pretty high attack value, and the 'rapid fire' ability, which means it can fire twice if it doesn't move during its turn. It needs to be kept away from the enemy, though, as its defence is even lower than the mimes'
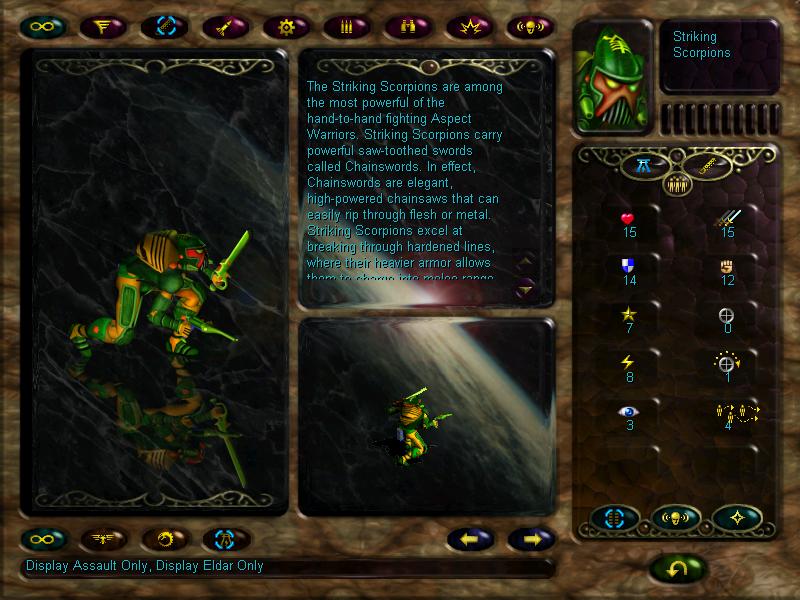
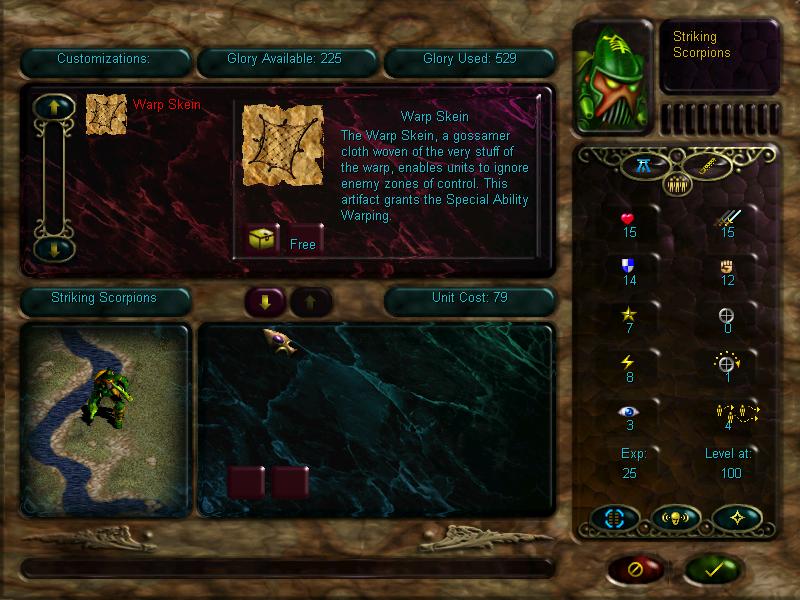
Striking scorpions will be our shock troops. They have decent movement rate, excellent defence, and very good melee damage.
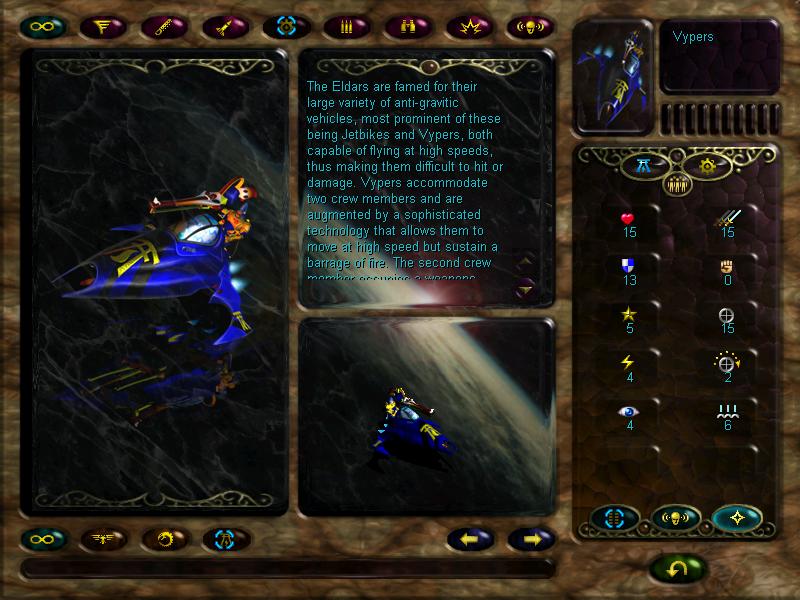
And finally, vypers are early hovertanks. Excellent movement, good damage, bonus damage when striking from forests thanks to the pop up attack ability and a range of 2. Pretty useful to scout along with the mimes.
Unfortunately, I didn't have enough glory for a vyper, so the current strike force is as follows: 2x striking scorpions, 2x fire dragons, 1x mimes, 1x scatter laser, 4x guardians.
Let us start the mission.
Soundtrack:
1:01 - 5:15
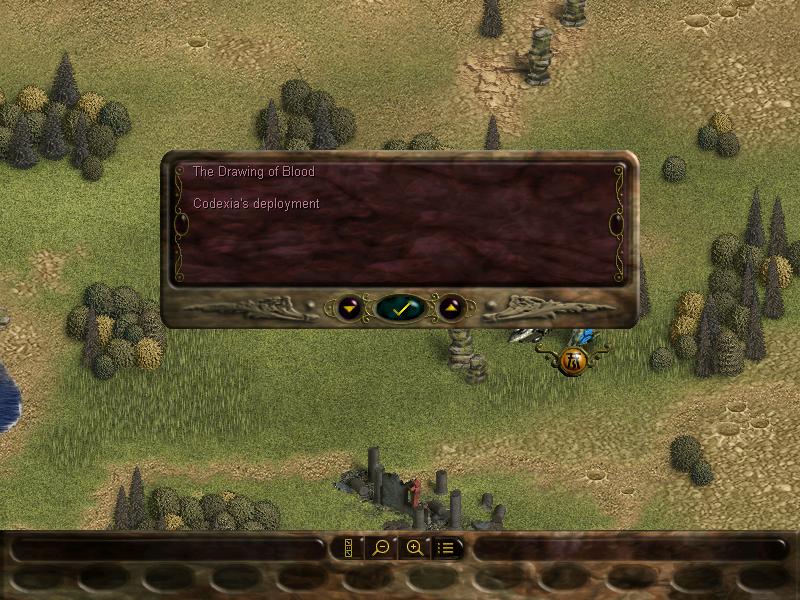
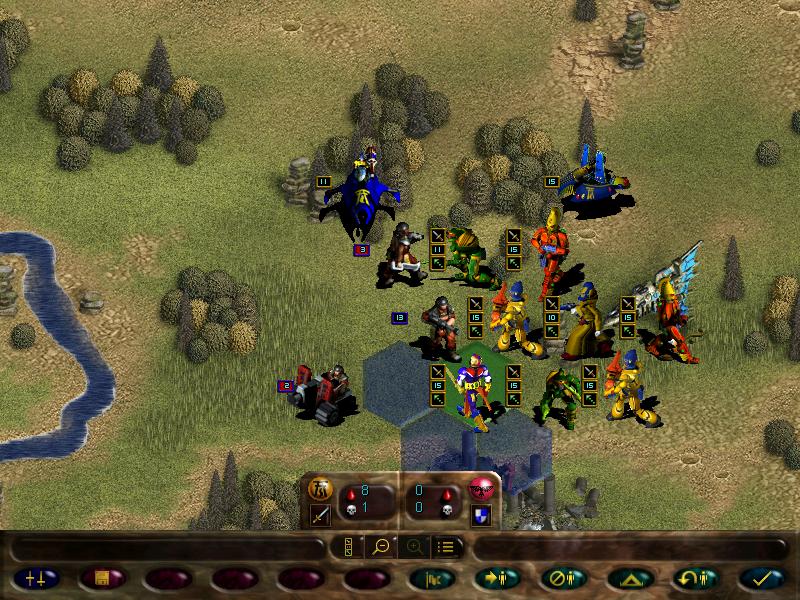
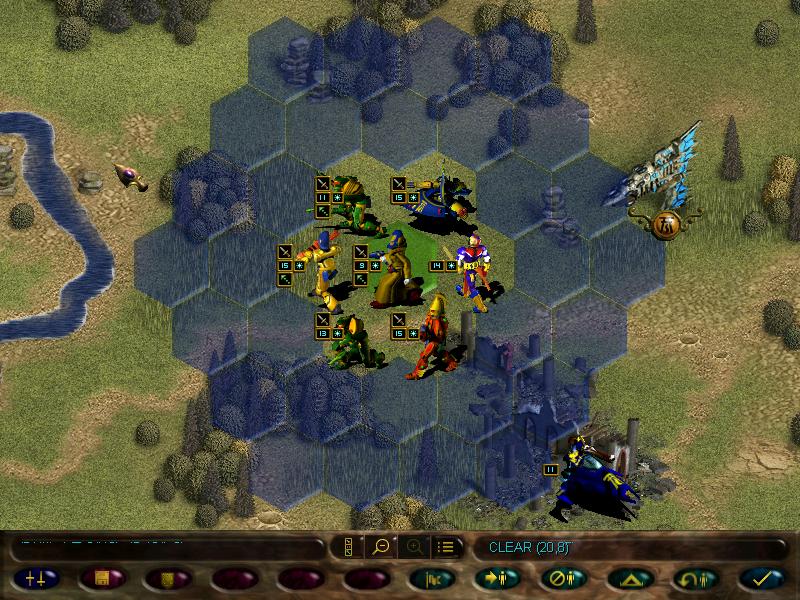
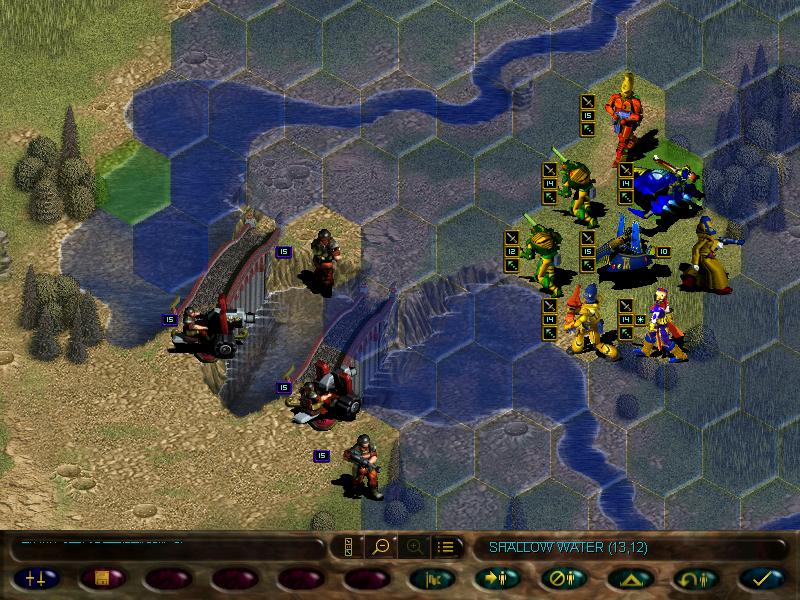
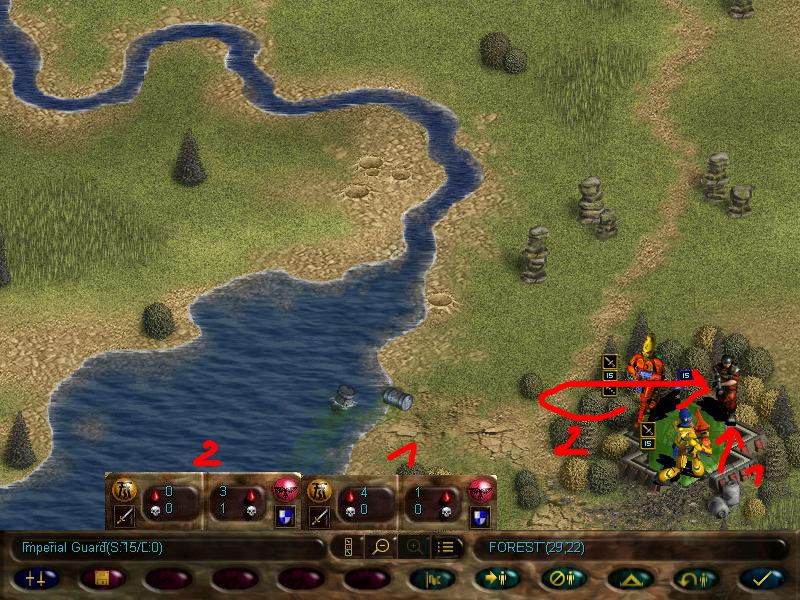
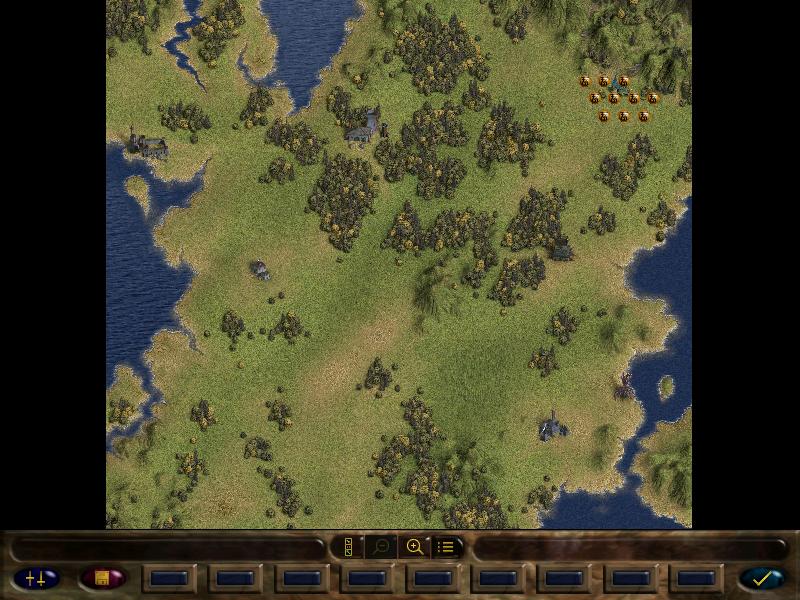
Here's the map. The yellow dots with eldar symbols are our bros.
During deployment, we can shuffle the units to get a better starting formation (vital later on, as there are missions where our starting position will get stormed from the get-go)
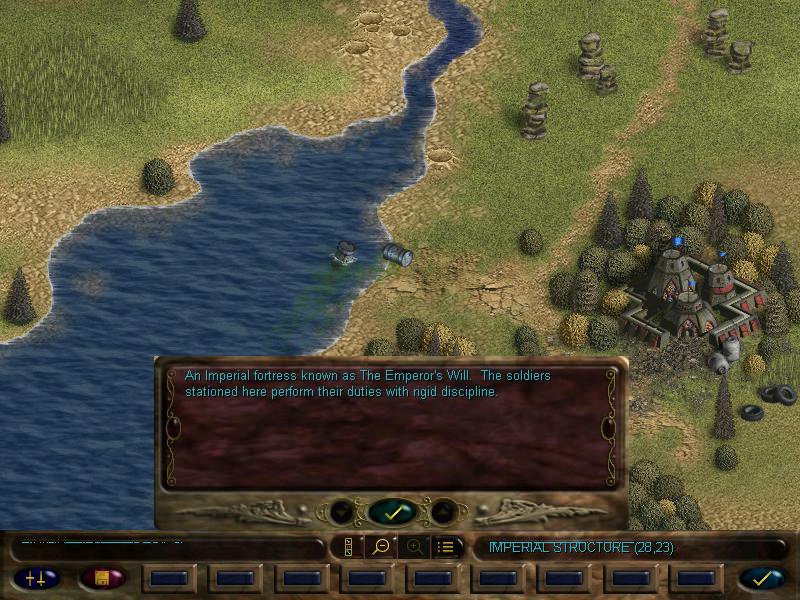
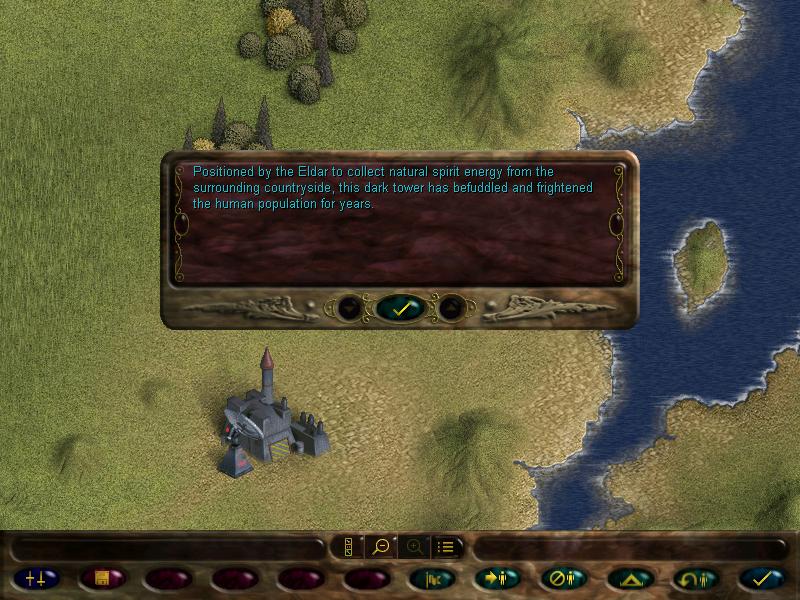
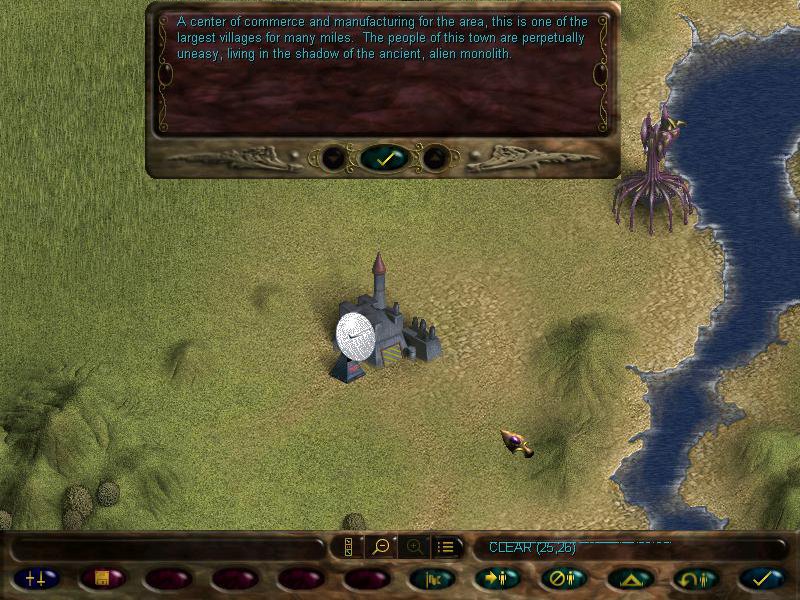
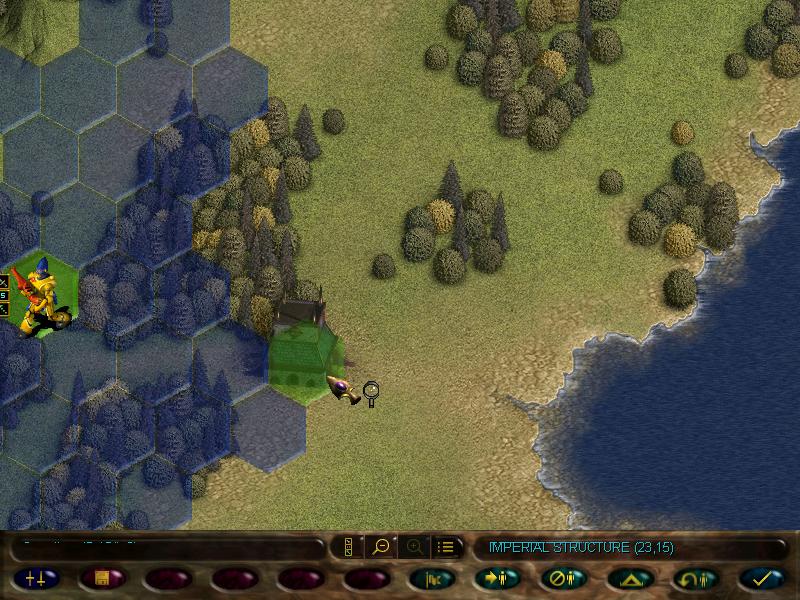
There's also a couple of key locations on this map. This Eldar spire:
And a couple of Imperial towns:
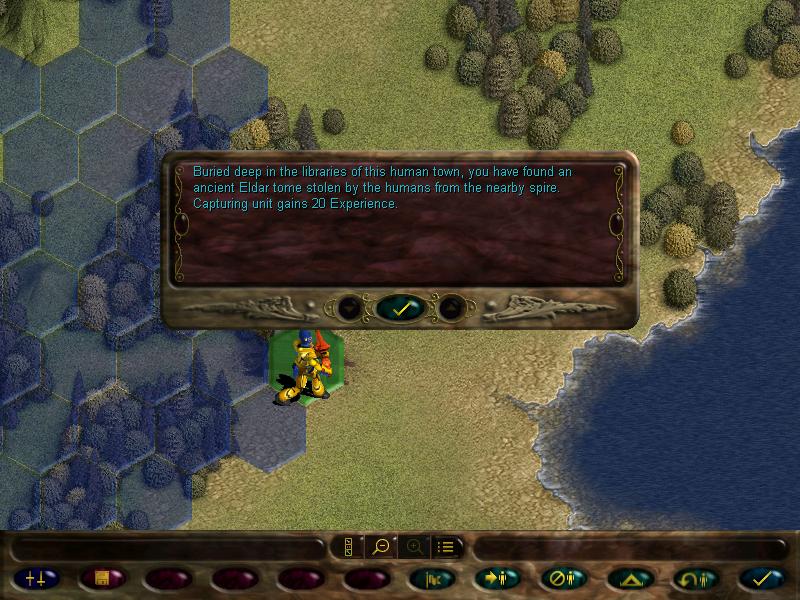
Invading those sites may give us various bonuses. Some may hold artifacts, some can give us experience and glory, other can even hold imprisoned units we can liberate, but some can even be traps, holding enemy units and exploding booby traps. But they don't always have these things, sometimes they can be just flavour.
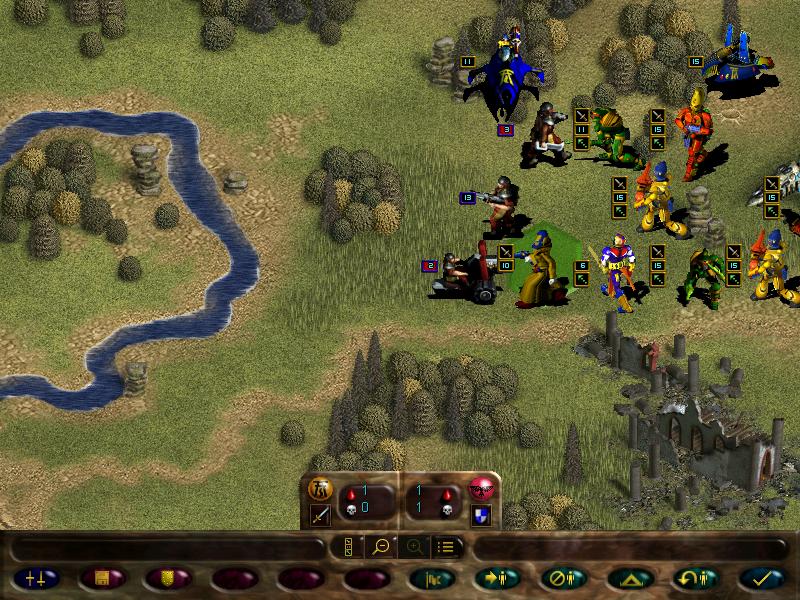
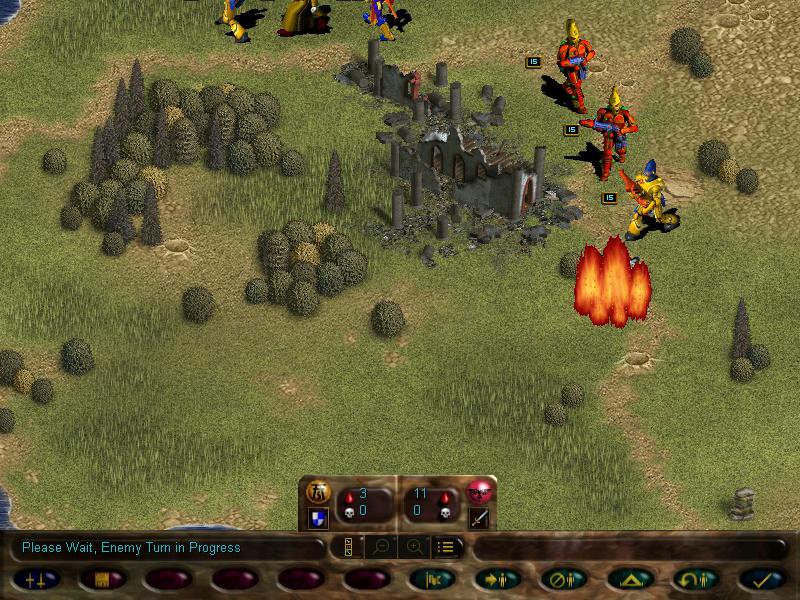
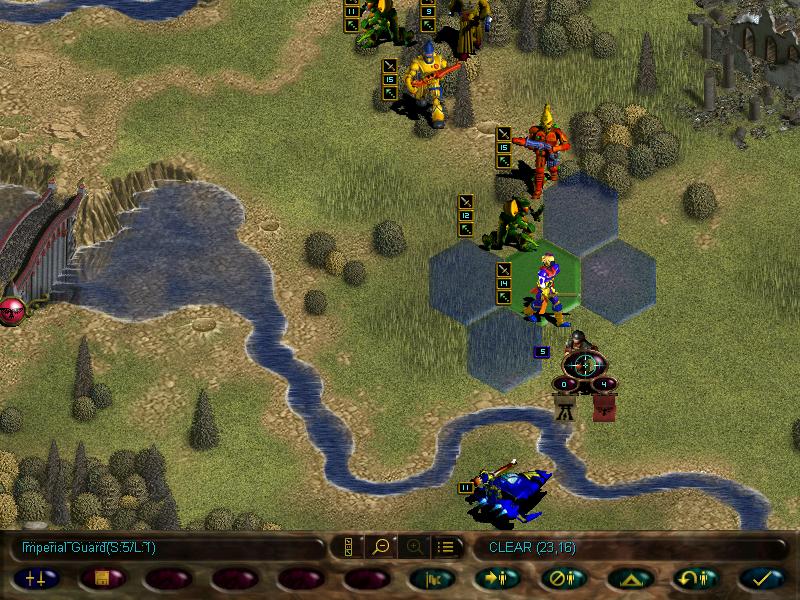
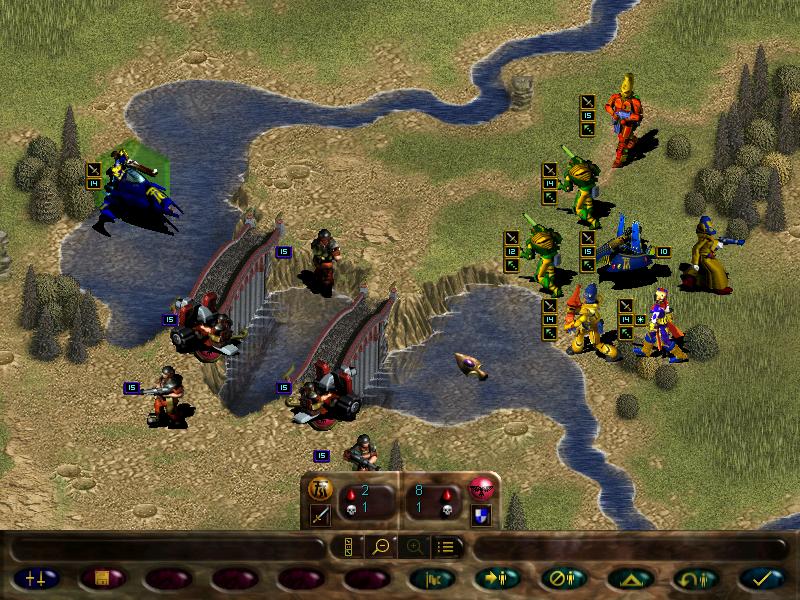
Thus, we start our movement and meet our first enemy...
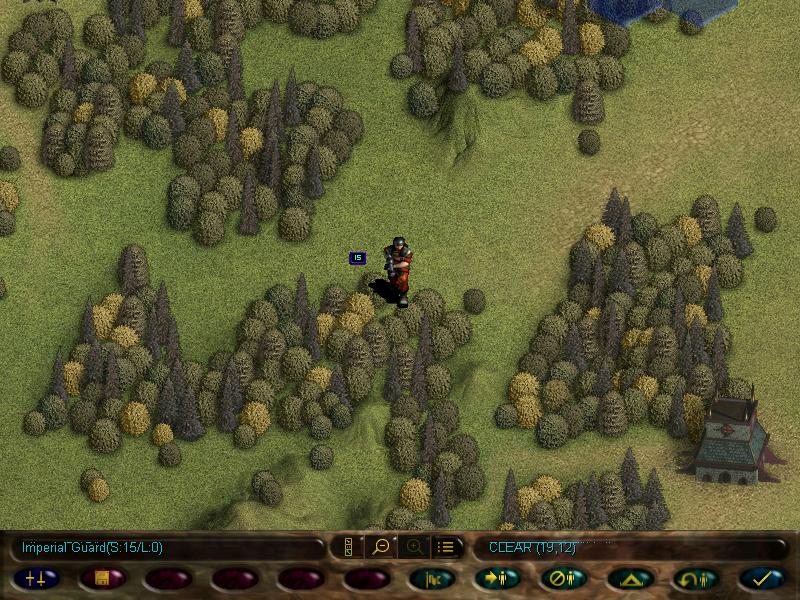
THE DREADED IMPERIAL GUARDSMEN SQUAD!!!!!!!
These boyz are the Imperial equivalent of guardians. Useless as shit.
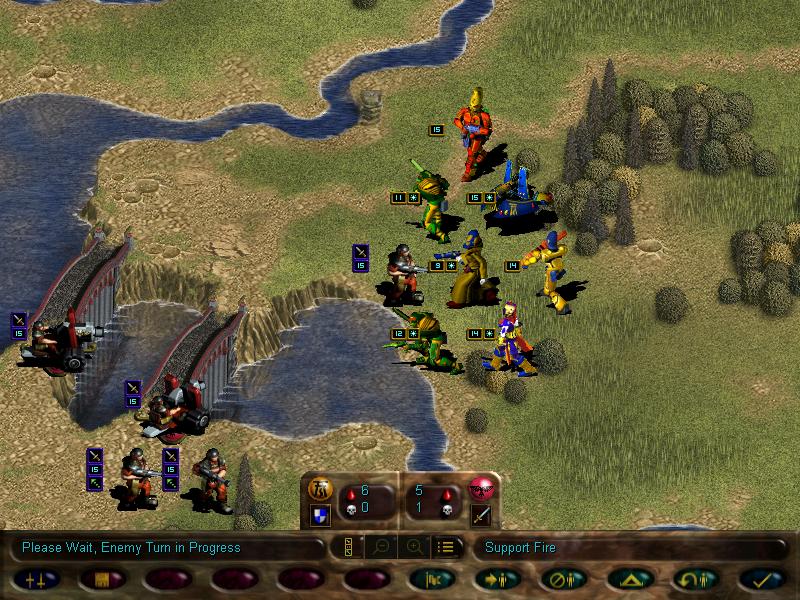
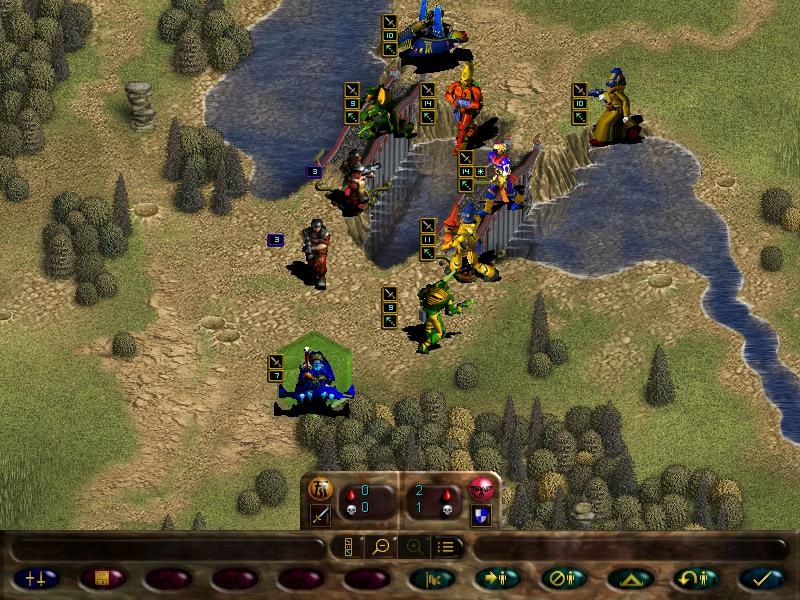
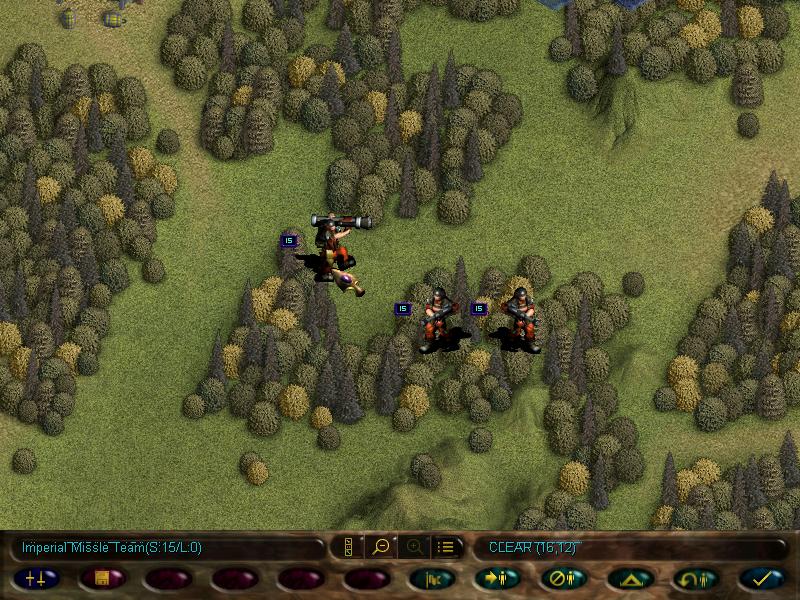
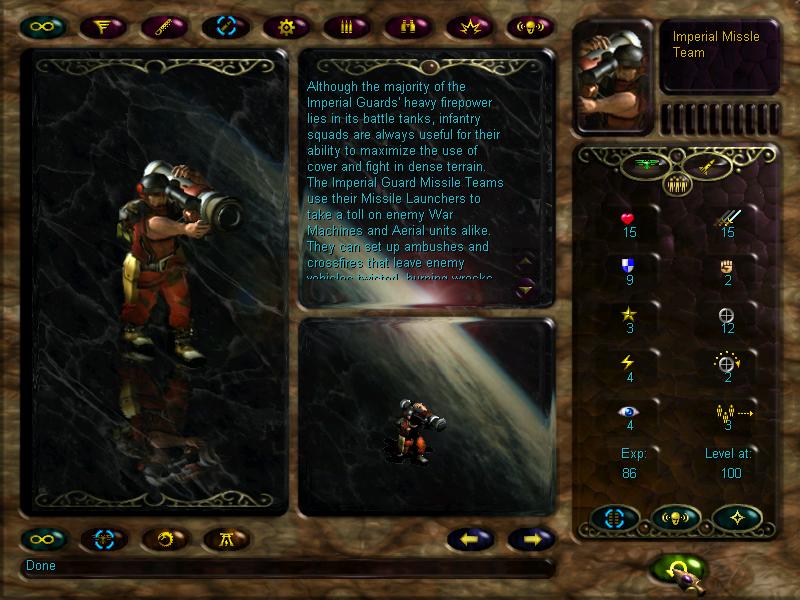
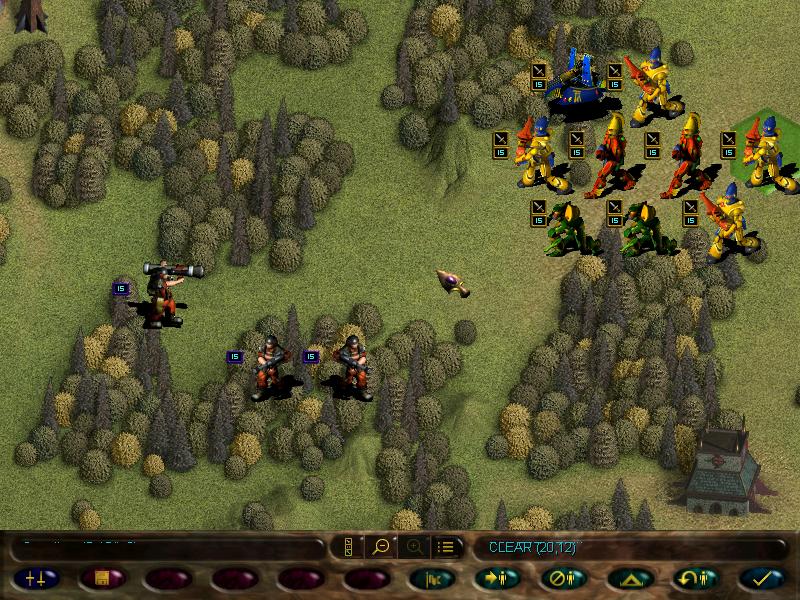
Going further down the map we spot more guardsmen, including a missile team.
Just like our fire dragons, these bros can launch support fire for friendlies, and have the armour piercing ability.
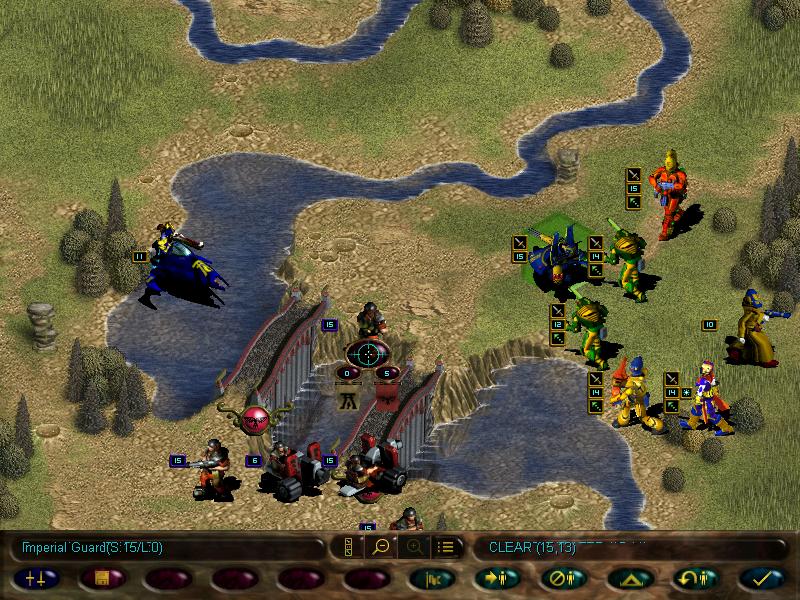
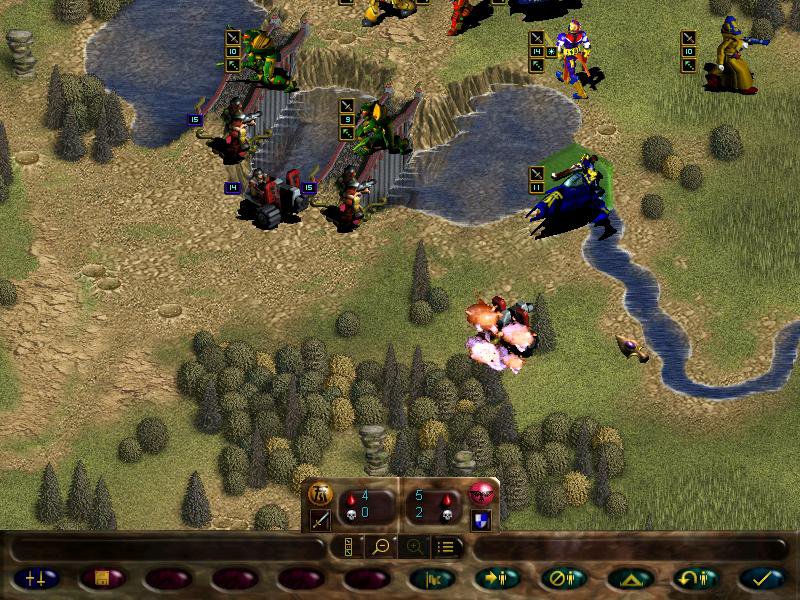
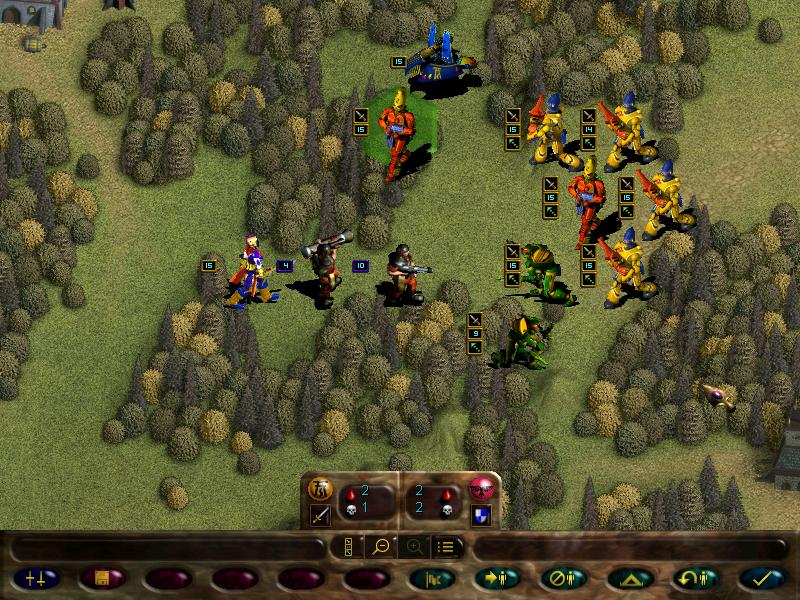
We move into a tight formation with fire dragons in the middle, and end turn...
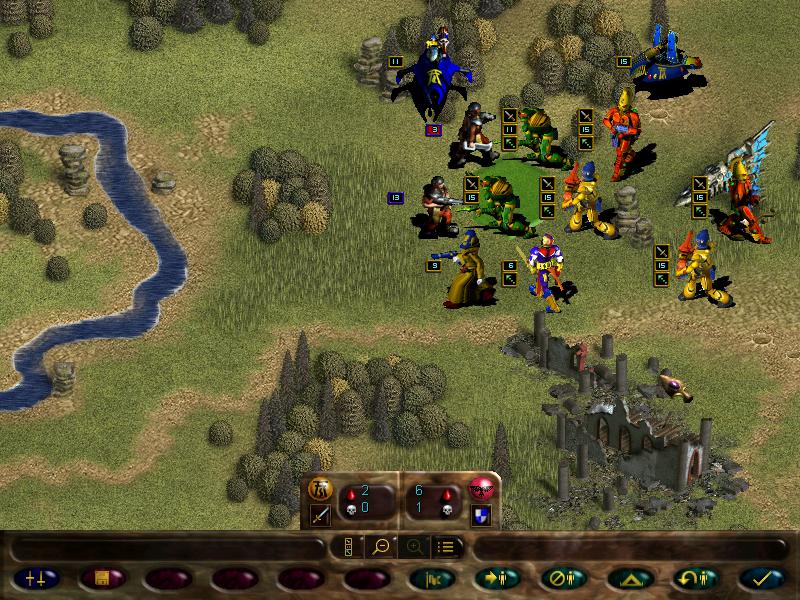
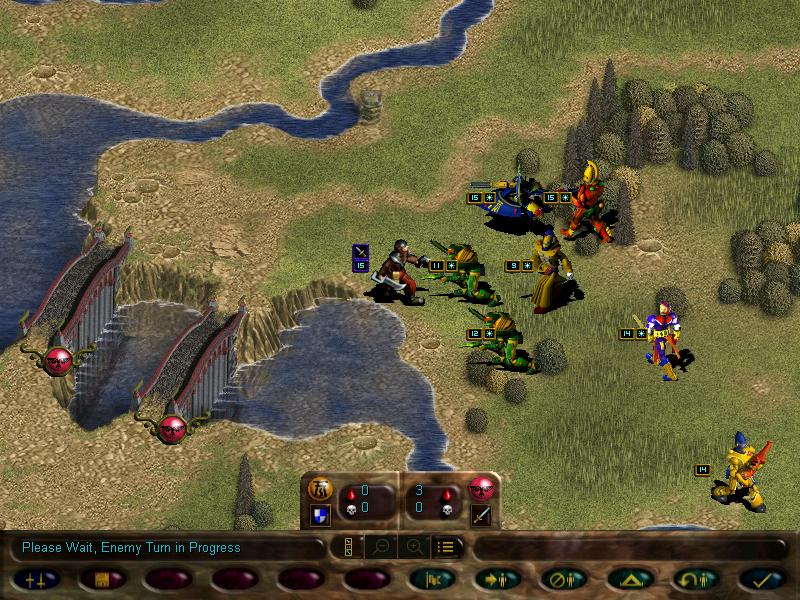
OSNAP, the bastards attack our guardians. Forgot to take the kill numbers, but it left our guardians at 10 strength, while the guardsmen are at 8 (thanks to the combined fire of guardians and fire dragons)
After that, the scatter laser uses rapid fire to eliminate the pitiful guardsmen.
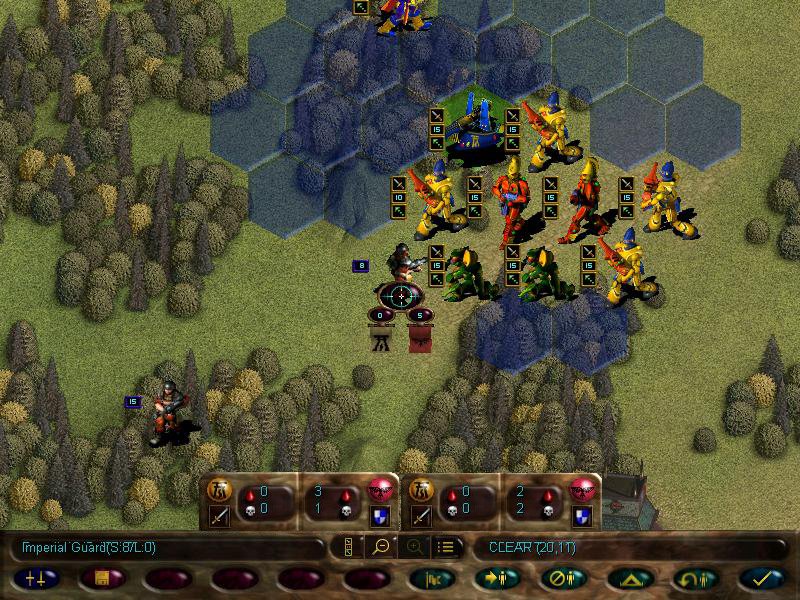
The blood drop and skull symbols on the combat windows show the amount of units wounded and killed. Wounded units can be replenished by resting for a whole turn, but to reinforce kills, you need to rest in one of the key locations.
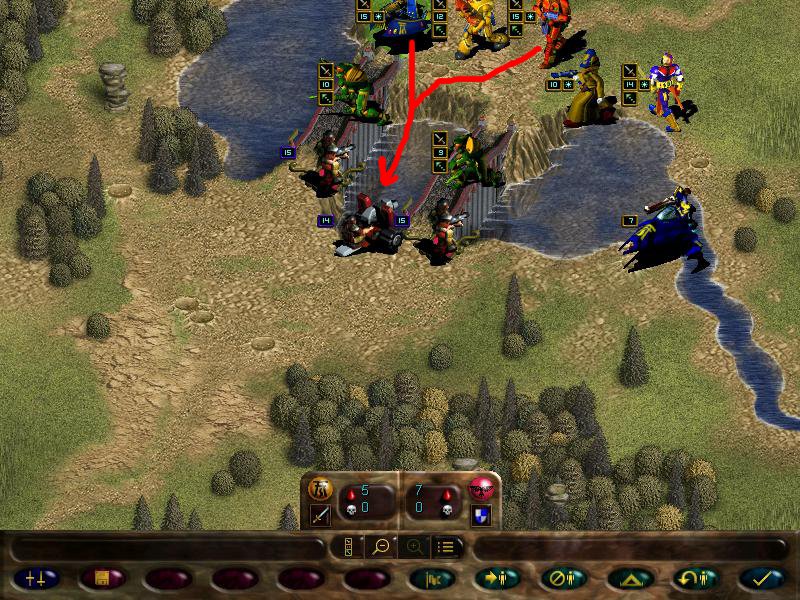
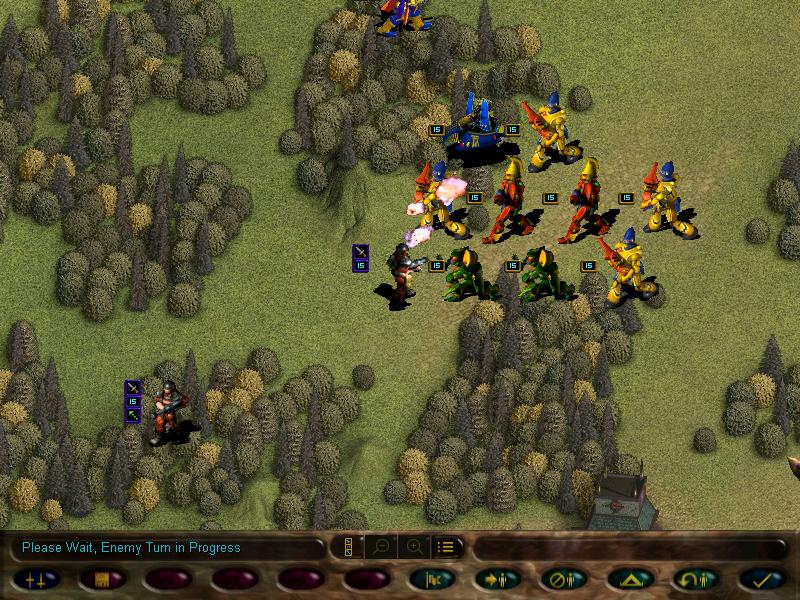
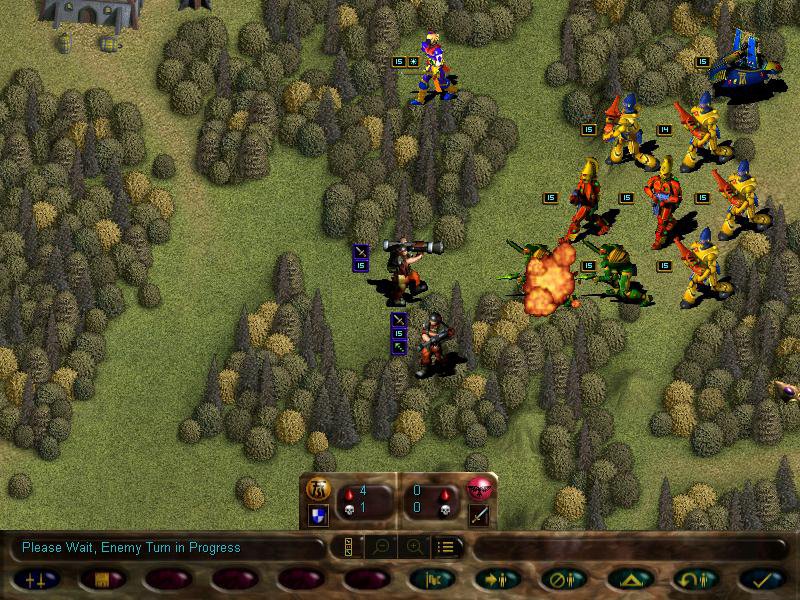
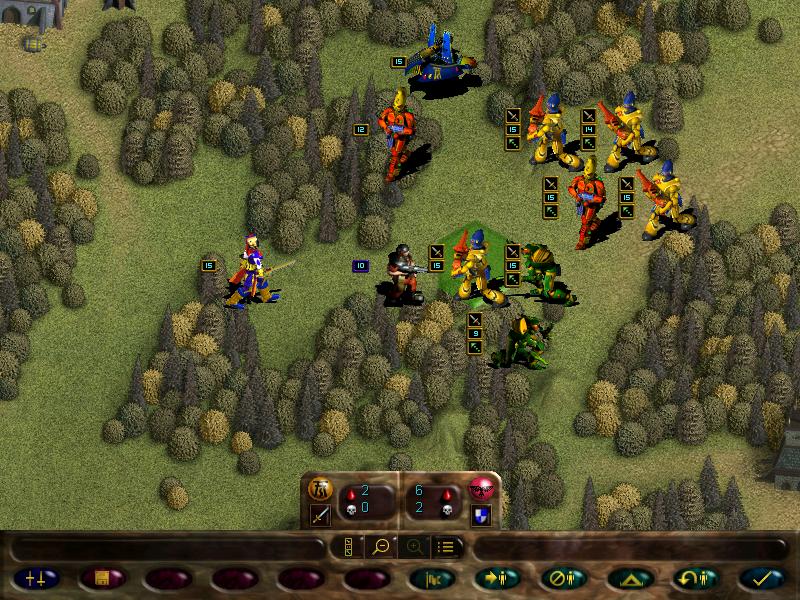
Later on, the enemy missile team shoops our scorpions
Guardsmen squad also joins in, but it suffers a lot more losses due to the fire dragons (melee squads such as striking scorpions cannot retaliate when under attack by ranged ones)
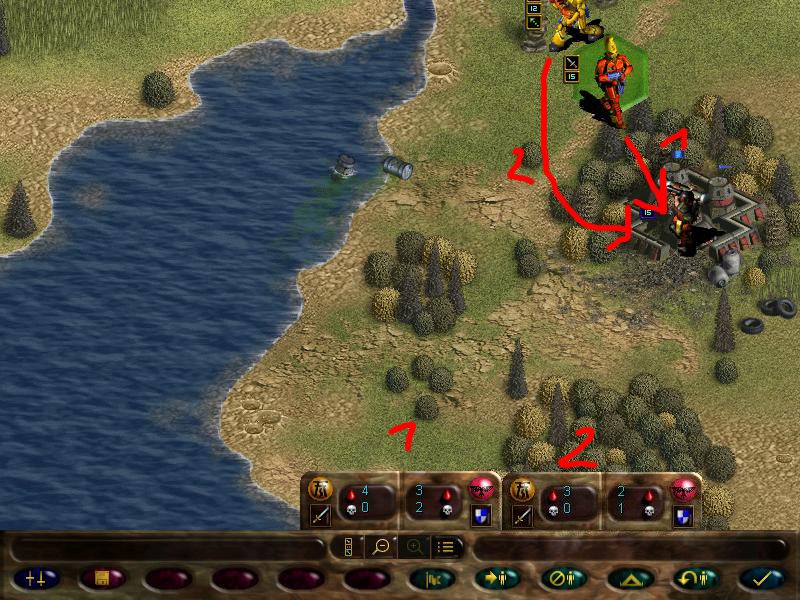
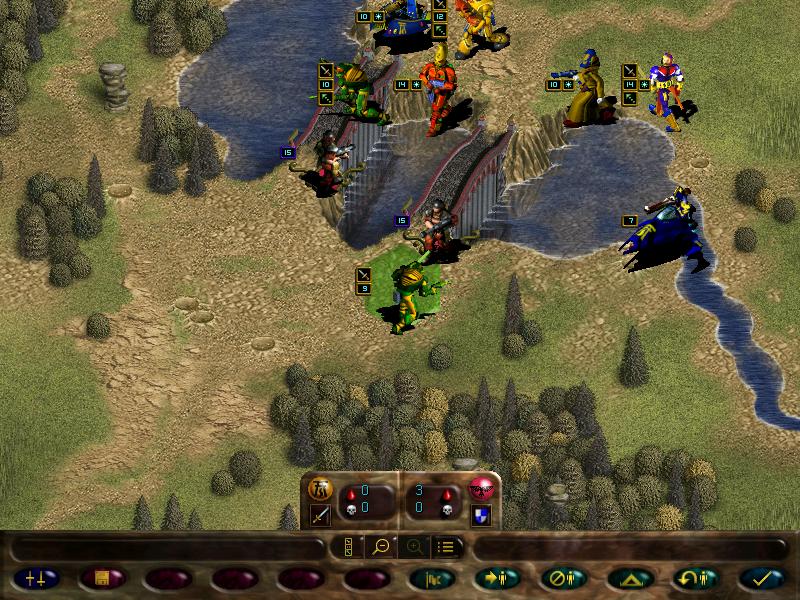
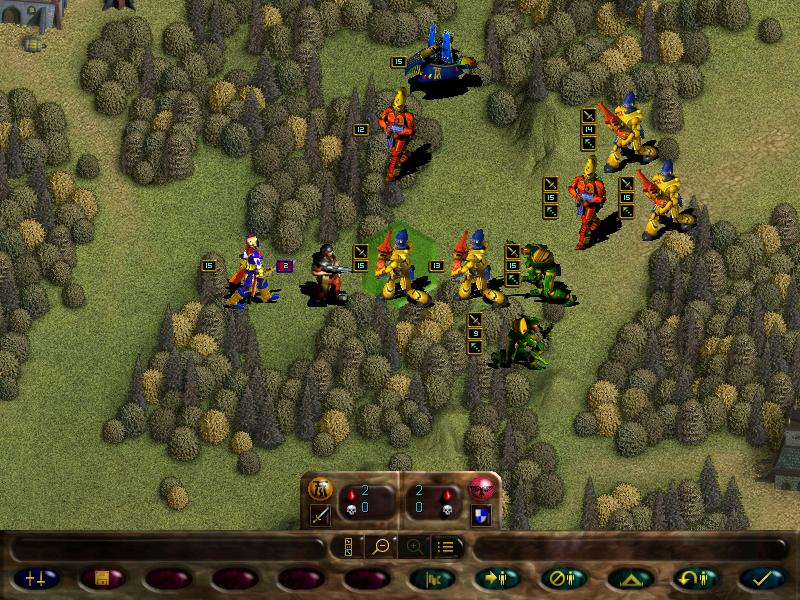
We use the mimes to outflank the missile team
Then we soften it with the scatter laser's superior range
And finally kill with fire dragons.
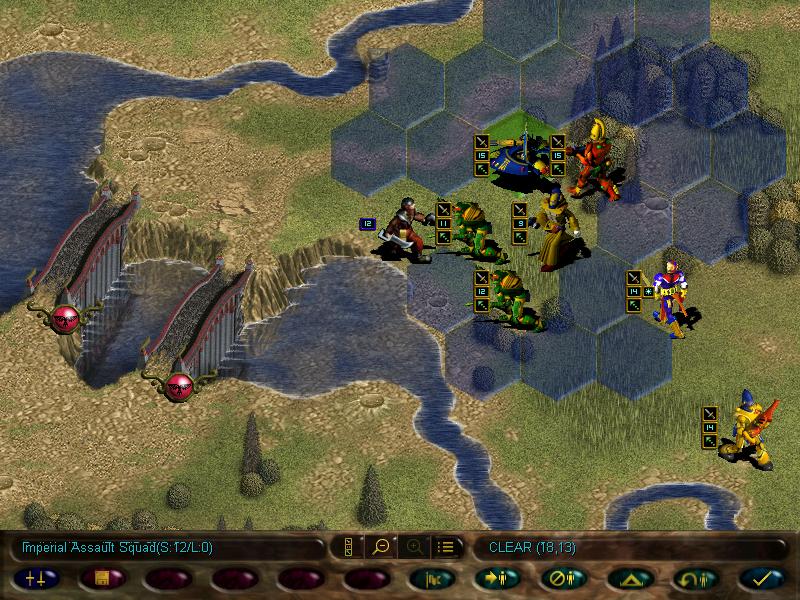
Then we crush the guardsmen
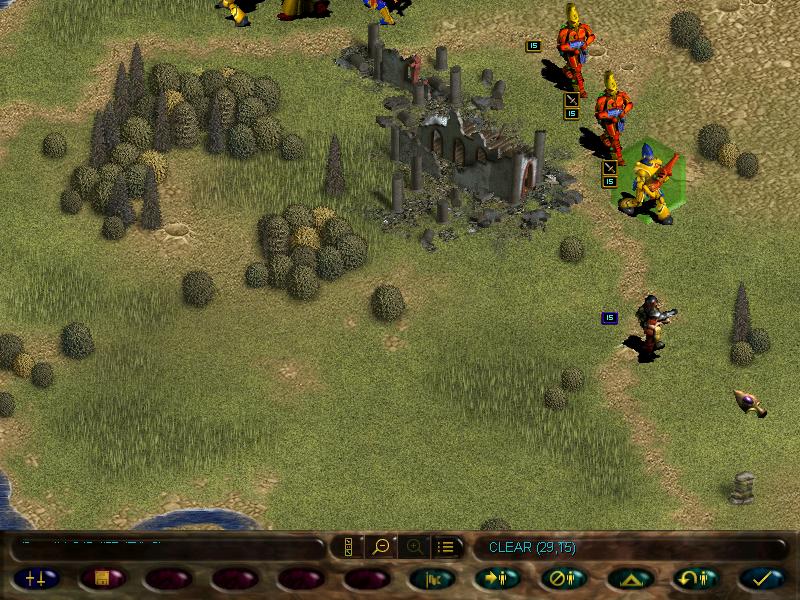
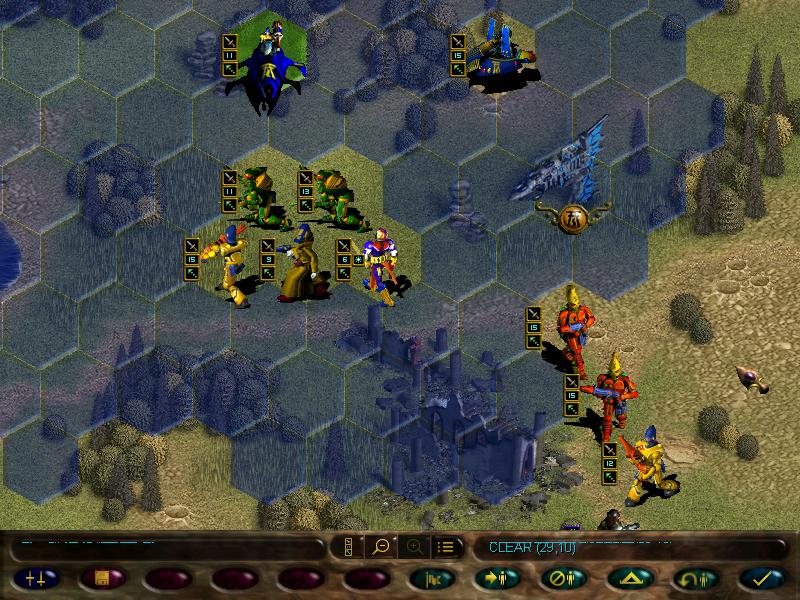
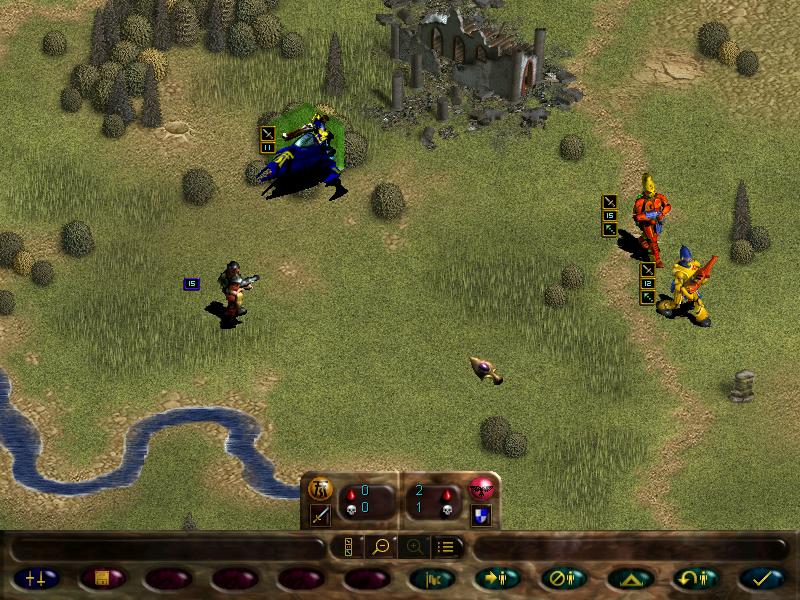
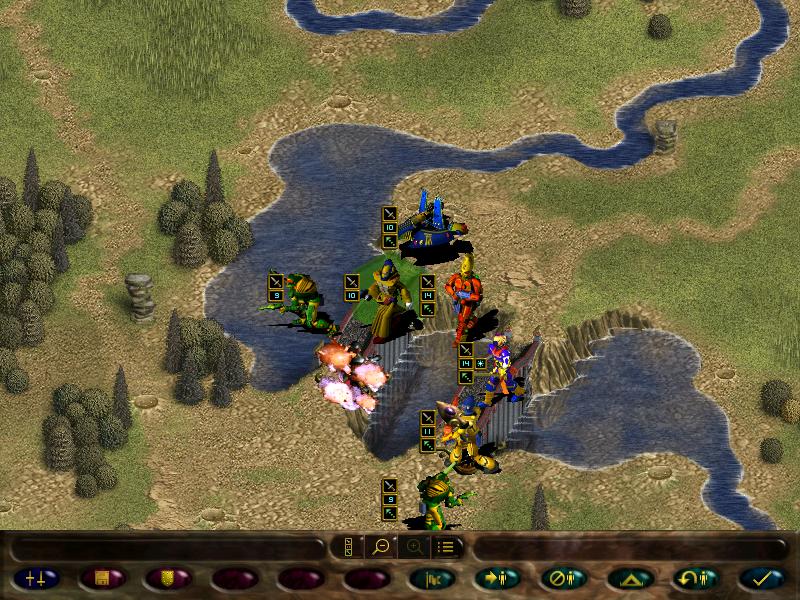
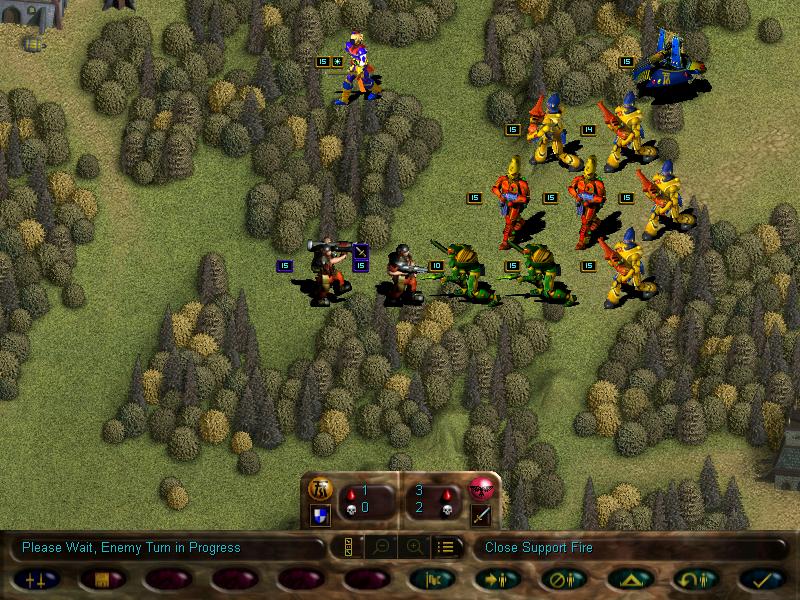
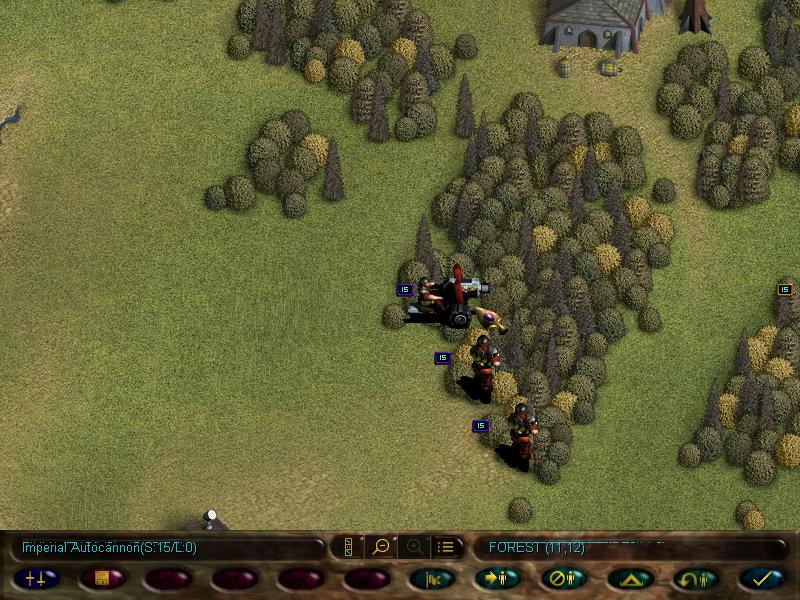
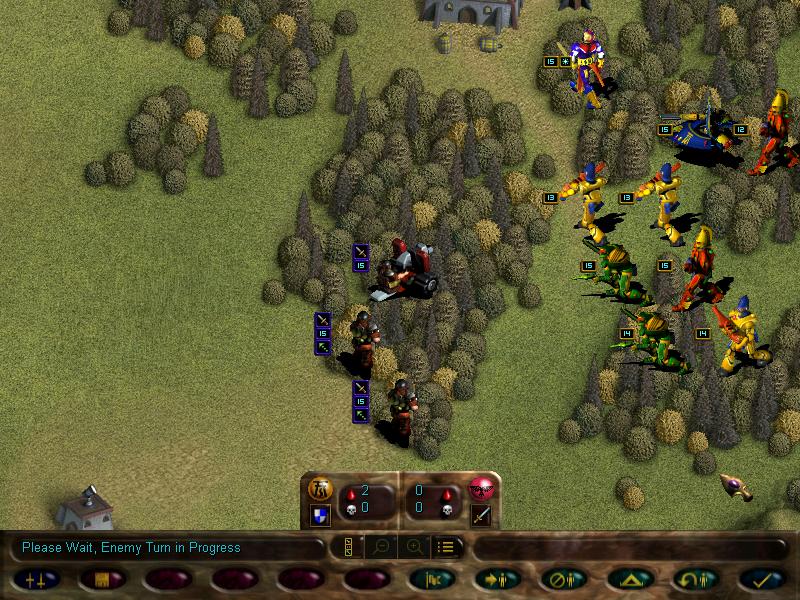
But all the fighting uncovered a new enemy force, including an autocannon!
This is pretty much the Imperial equivalent of our scatter laser, just more sucky.
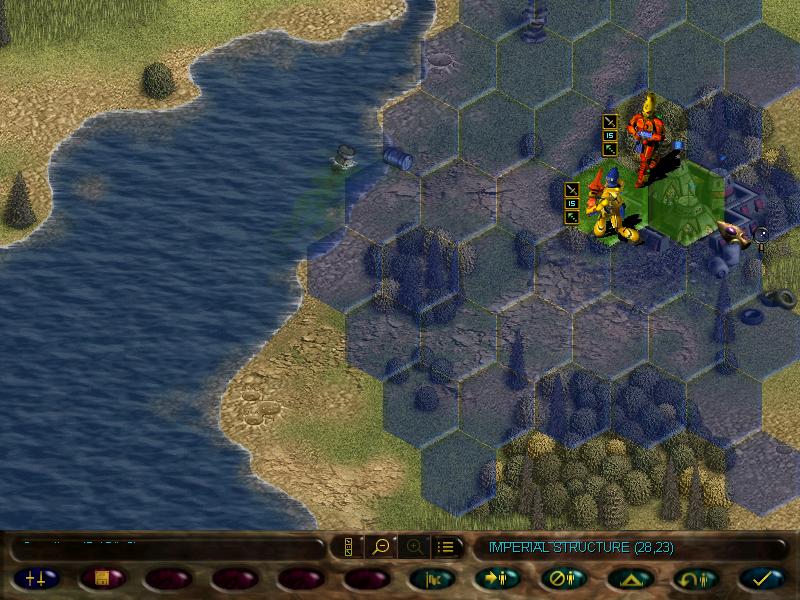
Let's check this village.
Cool.
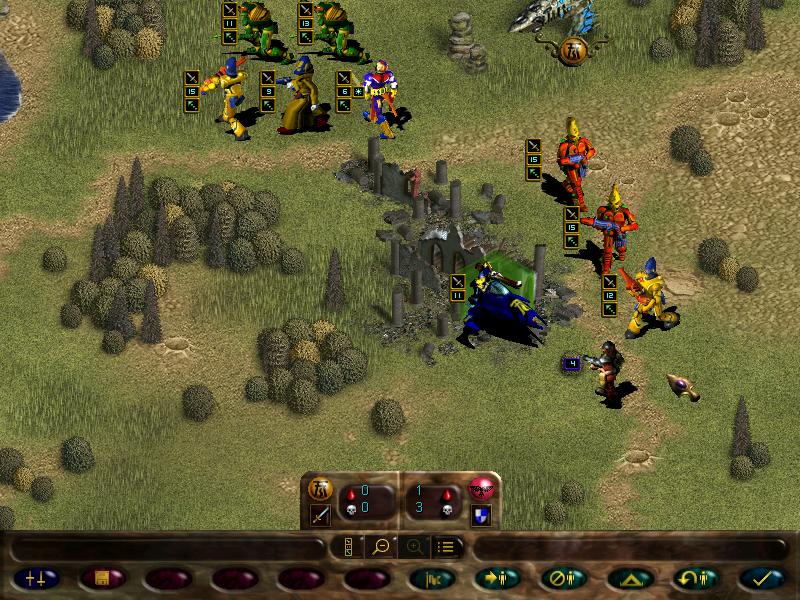
Meanwhile, the autocannon fires upon our guardians.
Another foolish guardsmen squad tries to do the same, but is burned down by the fire dragons.
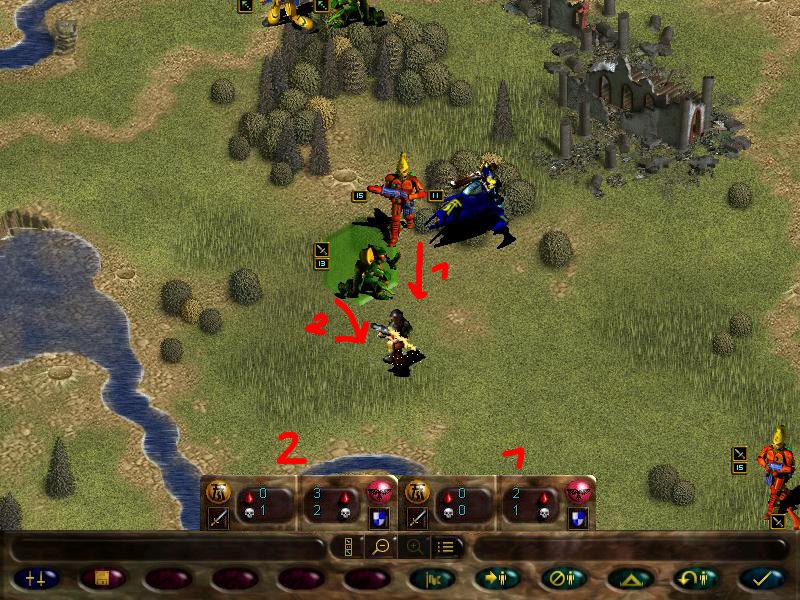
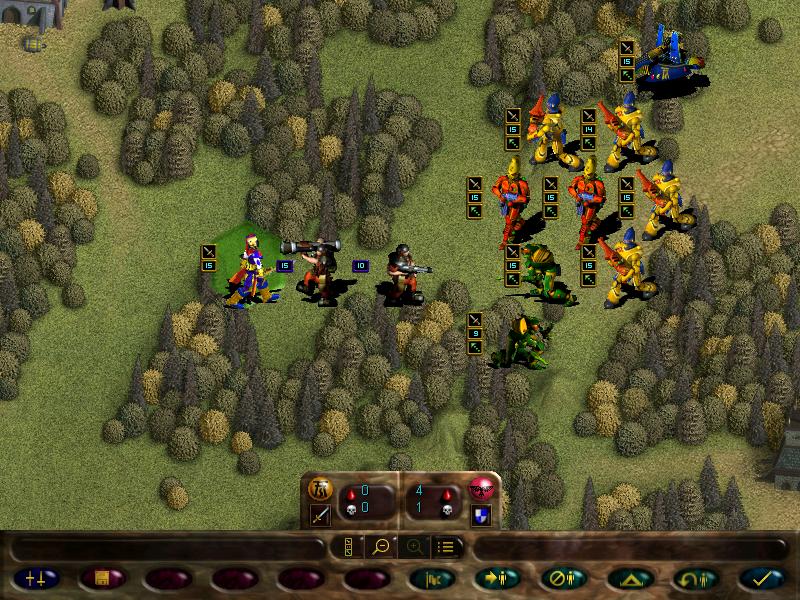
Mimes charge the autocannon
And the scatter laser finishes it off.
Then we dispose of the remaining guardsmen:
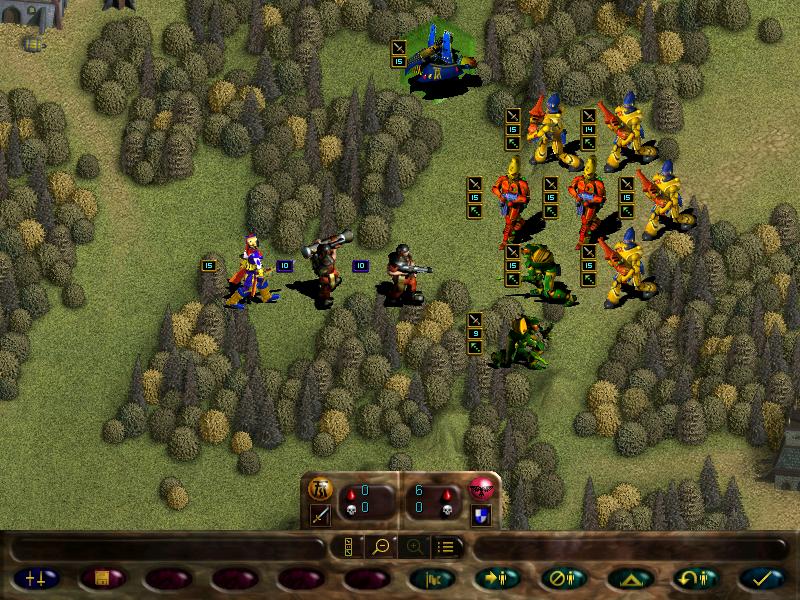
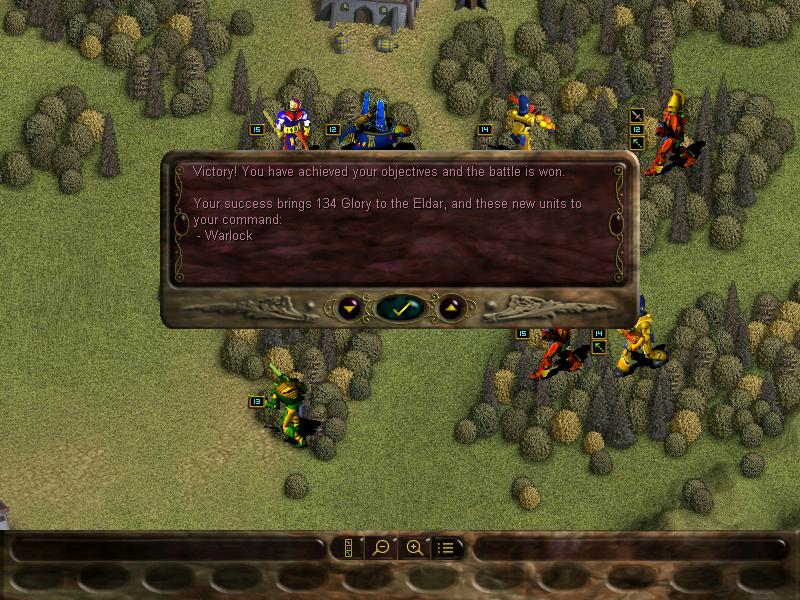
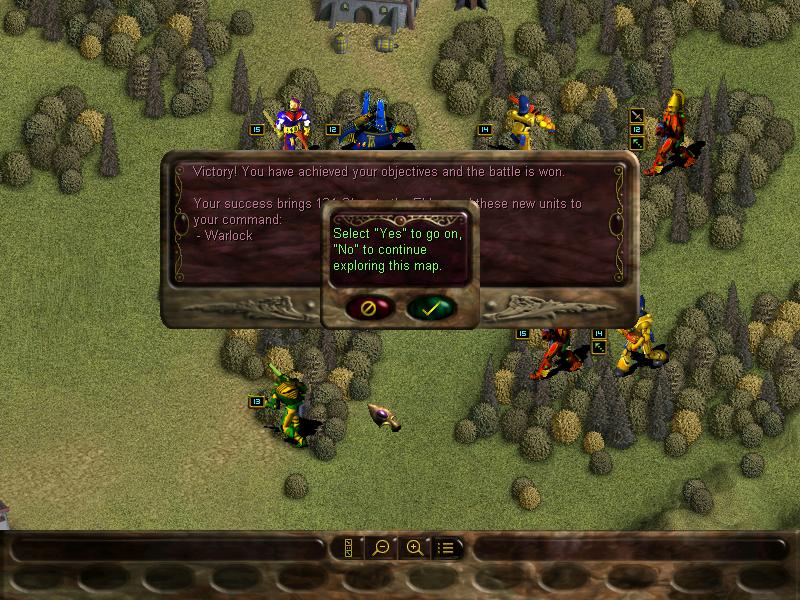
Aaaaand VICTOLY!!!!!
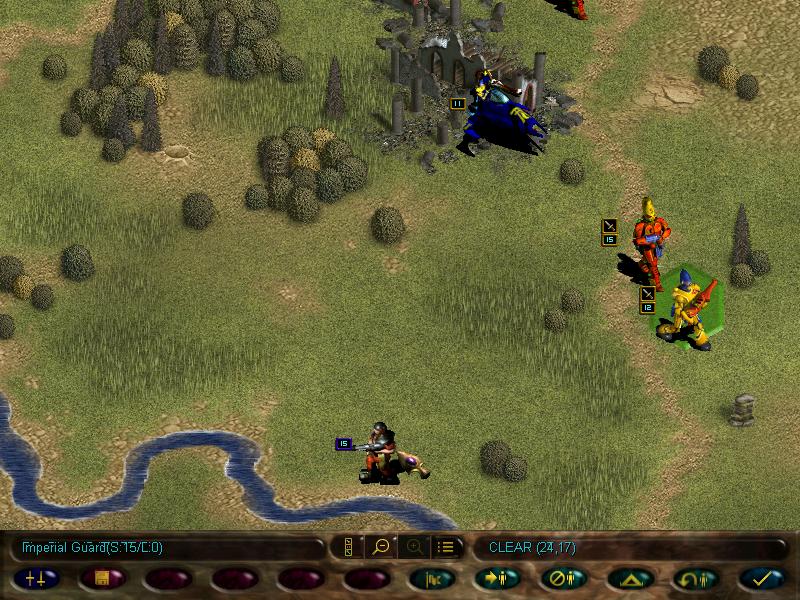
But we do not leave yet, no, there are still sites to visit.
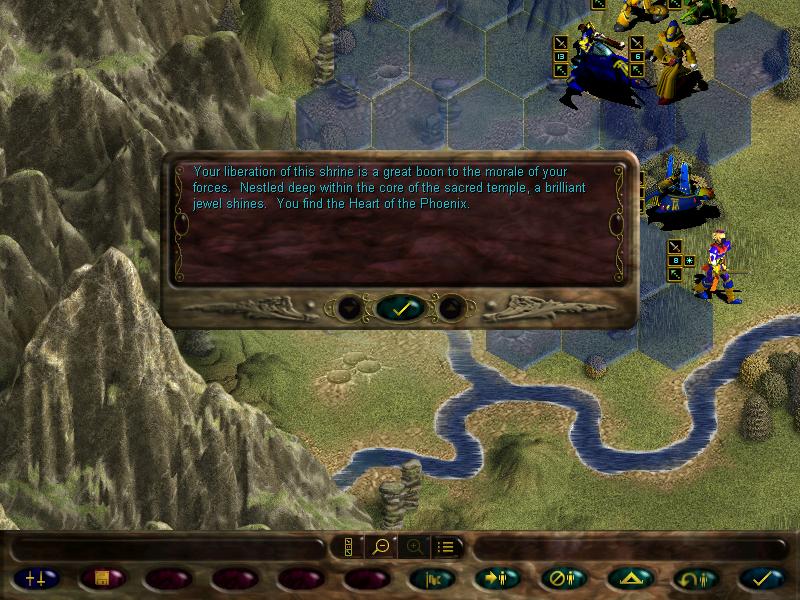
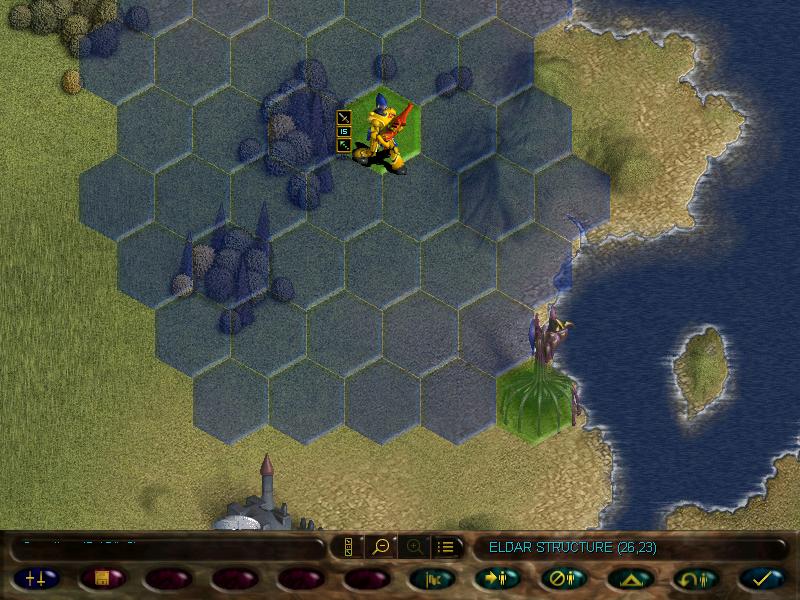
This Eldar spire:
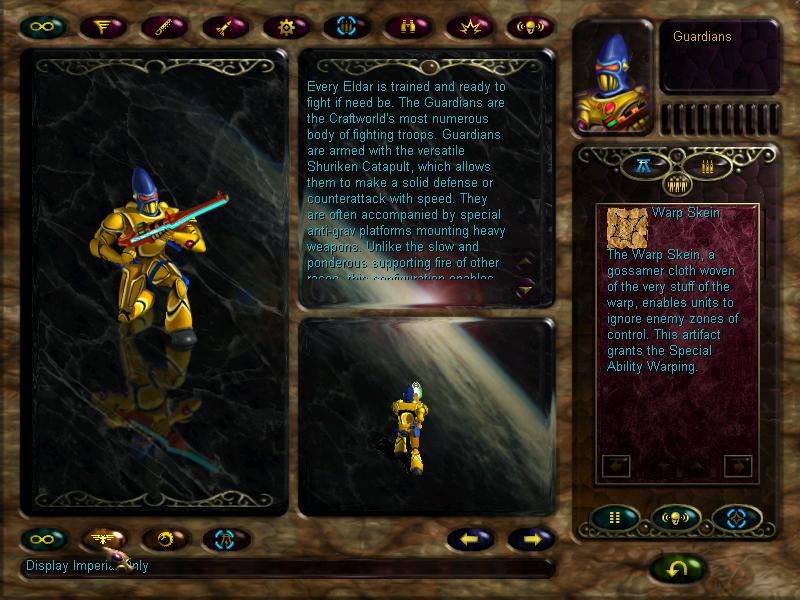
Cool.
In other words, this allows units to just move through enemies to get behind them. Think about Warp Spiders and their teleporting around and stuff, this is the same thing.
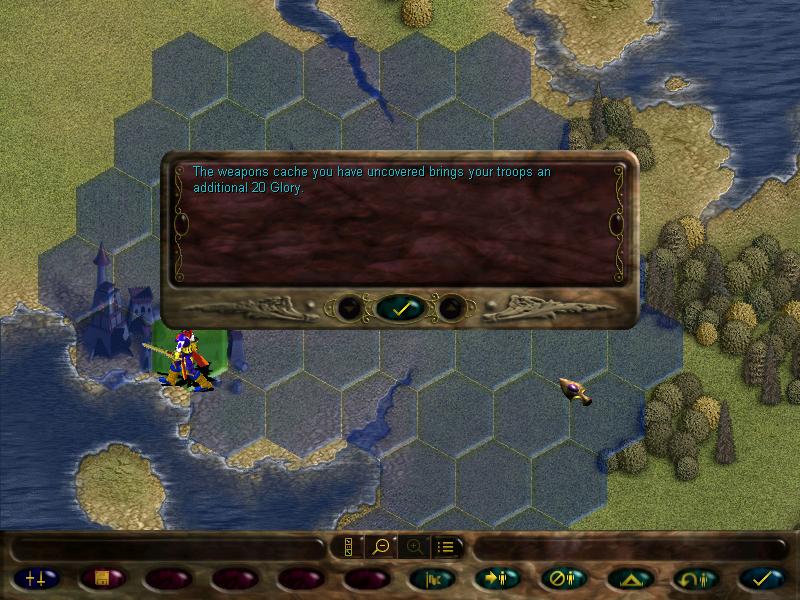
In another town we find GLORY, and that's it. All others are just flavour. Let us end the mission.
Another briefung.
Objectives.
First thing we do is give the warp skein to the striking scorpions, since the free movement profits them a lot.
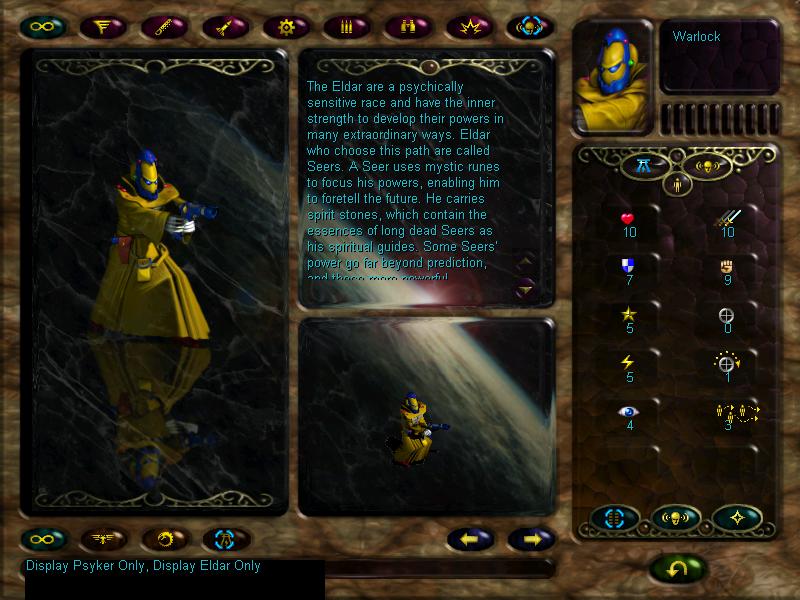
After that we check the new unit. A warlock. Our first psyker! Warlocks are pretty pitiful, they probably melt away faster than guardians, but once they get some levels, they can upgrade to warlock champions, later masters and finally farseers. All warlock upgrades are, pretty much, retardedly overpowered and the best psyker units in game. But right now, our warlock will be a little useless, but he has a nifty 'fortune' ability that increases the defence of all affected bros around him. He's also a single entity unit, which means he might have less HP than squads, but he doesn't suffer kills, and is immune to many nasty abilities that give +attack against squads/formation movement.
Thus we sack one guardian squad and get a warlock. We still lack funds to get a vyper, though

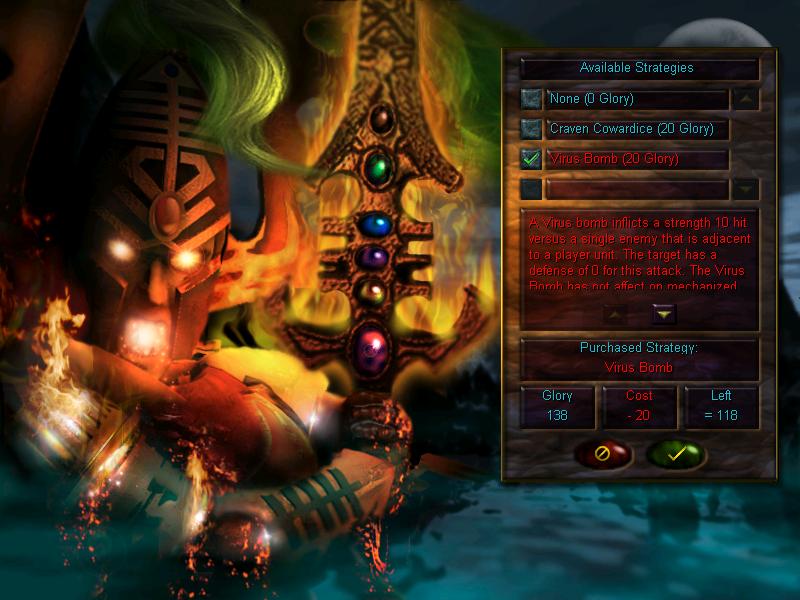
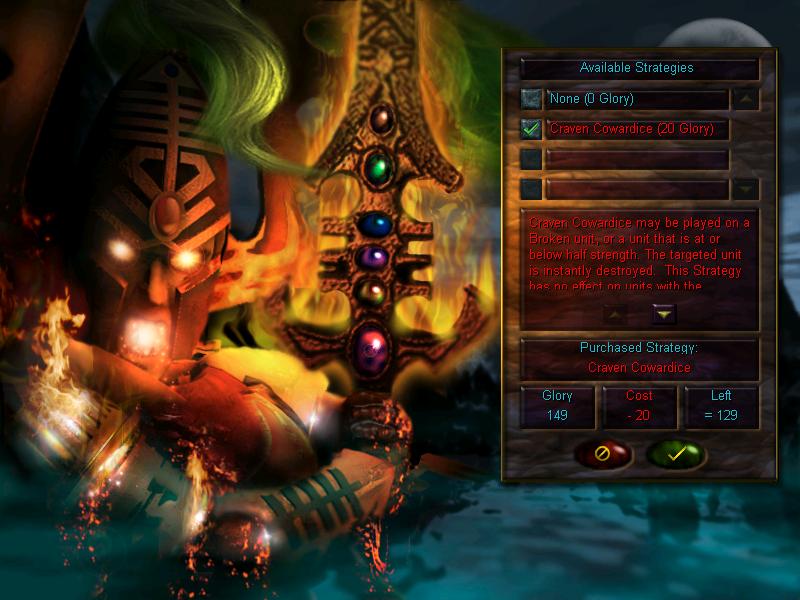
We can also buy a 'strategy' for the next mission. The only one available now is 'craven cowardice', which instantly kills squads that are broken or below half their strength. Has no effect on 'heroic' units (we won't be meeting those for a loooooooooong while) and mission-critical ones. It's mainly useful to quickly dispose of dangerous enemy squads that are attempting to retreat and rest.
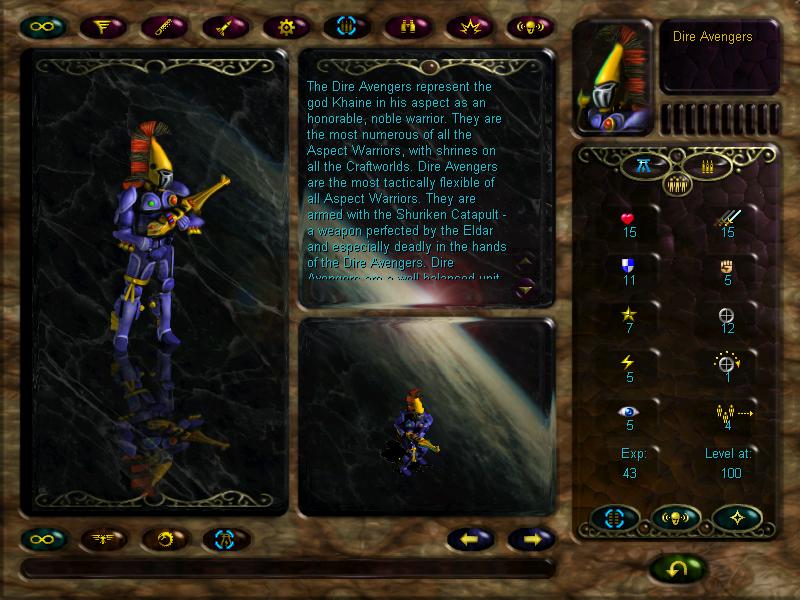
And this is where we shall end for now. In the next mission, we shall launch an offensive on Imperial bridges and liberate a lone squad of Dire Avengers. Stay tuned!
Also, from now on, I guess I'll just be posting the combat windows only instead of taking whole images of 3 units attacking the same one. If there's anything you'd like to see improved in the way I'm doing the LP, chime in.




















![Glory to Codexia! [2012] Codex 2012](/forums/smiles/campaign_tags/campaign_slushfund2012.png)

![Have Many Potato [2013] Codex 2013](/forums/smiles/campaign_tags/campaign_potato2013.png)
![The Year of Incline [2014] Codex 2014](/forums/smiles/campaign_tags/campaign_incline2014.png)