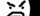Obsidian's Pillars of Eternity [BETA RELEASED, GO TO THE NEW THREAD]

[suejak]

Why not just give everyone a Bag of Holding. I always loved those in IE games.

Anyway, does the game have a title yet? They're not actually gonna call it PE, are they?

Well, it doesn't come out for well over a year (at best), so I dunno that there's much rush.

 

[Weierstraß]

The stash is not so much a problem of gameplay and balance as it is a problem in presentation. Games do not need to be completely realistic but a bag that I can put things in, but somehow instantly scrambles in such a way that I can not get things out just doesn't work for me.

 

[imweasel]

Personally I wouldn't mind if you had to find/fight for/buy them either...

True, that would be better than just a generic stash. Much better.

The bags of holding were fantastic rewards in BG2 and I loved them. The gem bag was also cool.

 

[PlanHex]

The stash is not so much a problem of gameplay and balance as it is a problem in presentation. Games do not need to be completely realistic but a bag that I can put things in, but somehow instantly scrambles in such a way that I can not get things out just doesn't work for me.

A Wizard Did It™

 

[Kirtai]

The stash is not so much a problem of gameplay and balance as it is a problem in presentation. Games do not need to be completely realistic but a bag that I can put things in, but somehow instantly scrambles in such a way that I can not get things out just doesn't work for me.

Just say that it's strictly FIFO, so if you want something you put in 50+ items ago, you'll need a lot of time and space to pull out everything that went in after it. The Ethshar books had them.

 

[Arkeus]

To give a more concrete example of how the original armor system could theoretically scale well but wind up in "What should I do?" circumstances:

The first table assumes you are equally proficient/damaging with every weapon, i.e. the weapons all do their "base" damage with no modifiers. Relevant information:

DMG* = Damage Multiplier, per hit
Min/Max Dam = What it says, currently set to identical values to make editing easier. Values are arbitrary, differences between values are not.
Rate = Attack rate, though if it says DWF = 2, that means they can strike at twice the rate. In practice, two "fast" weapons will attack three times for every two times a pair of non-fast weapons attack, and three times for every one that a 2H weapon attacks. 3:2:1.
DT- = How much DT is negated by the weapon as a base value. This scales with DMG* to prevent the value from becoming irrelevant. Piercing weapons only.
MDTDT = Minimum Damage Through Damage Threshold. Multiply this by the initial damage to determine the minimum amount that will get through armor, no matter how high the DT. Proportionally increases with weapon size and is doubled for crushing weapons.
DWF = Dual Wield Factor. 2 = Yep, they can be.

As the spreadsheet hopefully indicates, things scale pretty much as you would suspect, but it is a graduated process. At the very top and very bottom ends of the spectrum, the right tools are pretty clear... assuming all of your DMG* are equal. The second table shows what happens when a small range of DMG* variability is introduced into the equations. As the DT rises, it still kinda sorta holds up, but there are aberrations: Fast Piercing weapons are much more dominant in the mid range from a 20% increase to damage and an additional 4 points (20% of 20) DT bypass. In some cases, the differences are minor, but in other cases, it makes a significant difference.

And ultimately, those DT values at the top and the names that correlate with them are base values. When you see someone in mail, you don't know that mail has 30 DT. It may have 35 DT. Or it may have 40 and the target is wearing a ring that grants +5 more DT.

To be clear, I think this is a neat mathematical system and it's fun to play around with in spreadsheet, but I think it does pose some problems for players who are making tactical choices in a 6 vs. 6 (or more) scenario. I'm also not saying that the problems can't be solved, but I had tried a number of approaches and wasn't coming up with very satisfying solutions.

SunBroSolaire, on 24 Jan 2013 - 01:58, said:

50% seems like a really harsh penalty. I would assume crushing weapons aren't getting the -50% applied against light/medium armor, which would mean carrying a slashing weapon would be a huge liability. If one third of the time it does moderately higher damage than piercing/crushing, but two thirds of the time does 50% less damage + potentially misses DT altogether, you're going to end up with a weapon that is basically useless. I can't imagine any reason to use anything but clubs and mauls in this scenario.

On the other hand, if crushing and piercing weapons ARE penalized against lighter armor, you have basically a game of rocks-paper-scissors.

I don't see what the problem was with the original system. Maybe you wouldn't immediately know what the optimal weapon would be in any given situation, but you could make a pretty good guess, and observing the combat log would basically seal it. I don't think it's intuitive at all for some weapons to just not work against some armor. In the old system, it sounded like you would be able to get by with a suboptimal weapon. In this system you HAVE to match up the damage type and armor type.

Josh and Tim obviously know better than me, since they've been playing with the system; this is just how it appears to me.​

Well, we're going to try this system out, but I do admit that I'm not 100% sold on it. I was really having a lot of trouble working out the wide variation in values in the original system (I made a post with the spreadsheet on the previous page) after adjusting formulae and values for weeks. If we do "go back" to the original system, it will need to include some remedies for communicating relative damage in the interface. At the high end of the DT spectrum, the decrease in damage is 90% over initial values for fast Slash/Pierce weapons, the worst of those (the fast Pierce, e.g. Stiletto) being less than 1/6th the value of the ideal weapon: the two-handed Crush (e.g. Maul).

 

[Hormalakh]

Thanks Arkeus. Someone brofist this man.

 

[Infinitron]

Instead the damage should be determined CHIEFLY by HOW you use a weapon than what weapon is it.

Uh, what you're asking for here is a system that would be more like Fallout than the Infinity Engine games.

IE games didn't have a scalable weapon skill that determined how well you used each weapon - only a relatively unimportant binary weapon proficiency. You either knew how to use a weapon well or you didn't.

Suddenly fixing what ain't broke is a good thing?

 

[Infinitron]

Well, Project Eternity obviously will have an equivalent of BAB. What does that have to do with this discussion, though? BAB is about chance to hit, not about damage. This whole damage/DT discussion is about damage.

 

[Infinitron]

Okay, so you want a sword to do more damage if a player improves his skill for using swords. I'm saying the Infinity Engine games didn't work that way, so Project Eternity has no reason to implement such a system.

In a classical D&D-esque system, your damage is determined by your Strength attribute, not by your swordsmanship skill. Skill is for hit chance, not for damage.

 

[Infinitron]

Alright. Agreed. That is what I am trying to say. That swords should do more damage if the PC improves a character trait; is that okay? And Please do not assume that DnD is a model. It is not iddeal for computer games all the time.

Ah I see what you mean.

Yes, Josh hasn't really mentioned anything about Project Eternity's attributes yet.

lol if the end the game ends up having no attributes

 

[Infinitron]

Definitely agree with you there. It prevents many problems.

 

[Captain Shrek]

Definitely agree with you there. It prevents many problems.

And now can you tell that to Josh?

 

[Radech]

Okay, so you want a sword to do more damage if a player improves his skill for using swords. I'm saying the Infinity Engine games didn't work that way, so Project Eternity has no reason to implement such a system.

In a classical D&D-esque system, your damage is determined by your Strength attribute, not by your swordsmanship skill. Skill is for hit chance, not for damage.

swordsmanship skill could allow you to deal different kinds of damage(piercing thrust or crushing pommel/hilt strike), and the skill level would reduce the damage penalty - could also be tailored in a way to make less classic weapons like halberds more viable, since they are designed to cause three types of damage without much skill

 

[Infinitron]

swordsmanship skill could allow you to deal different kinds of damage(piercing thrust or crushing pommel/hilt strike), and the skill level would reduce the damage penalty - could also be tailored in a way to make less classic weapons like halberds more viable, since they are designed to cause three types of damage without much skill

In Project Eternity, such things would probably be implemented via special class abilities/feats that rely on the Dexterity attribute and/or character level

 

[Arkeus]

Ah I see what you mean.

Yes, Josh hasn't really mentioned anything about Project Eternity's attributes yet.

lol if the end the game ends up having no attributes

Actually, Josh mentioned that there would be attribute checks for dialogs, not skill checks.

 

[Infinitron]

Ah I see what you mean.

Yes, Josh hasn't really mentioned anything about Project Eternity's attributes yet.

lol if the end the game ends up having no attributes

Actually, Josh mentioned that there would be attribute checks for dialogs, not skill checks.

Actually he said he would prefer attribute checks over skill checks, if he was going to have such checks at all.

But yeah, that's the only time I can remember him mentioning attributes/stats.

 

[imweasel]

To give a more concrete example of how the original armor system could theoretically scale well but wind up in "What should I do?" circumstances:

The system is broken as Josh already noticed. He will need to create functions to make it work the way he wants. Making lists and messing with the numbers is just bullshit, you really need to use functions and a plotter. I personally don't see any other way to implement his system otherwise, because it is rather complicated. Simple linear and absolute value functions would work. i.e. for slash damage (using the system he proposed):

f(DT) = -( DT/(MAX DT/10) ) + MAXDAMAGE

You just adjust the function and define domains (if required) until you get what you want.
It could also be done by adding different types damage threshholds (piercing, slashing, crushing) to armor I suppose. That would be the simpler solution

 

[Roguey]

Actually he said he would prefer attribute checks over skill checks, if he was going to have such checks at all.

But yeah, that's the only time I can remember him mentioning attributes/stats.

http://forums.somethingawful.com/sh...d=17931&perpage=40&pagenumber=3#post407878166

I'd like to look into options to disable messages of that sort (skill checks, attribute checks, reputation gain and loss)

http://forums.somethingawful.com/sh...d=17931&perpage=40&pagenumber=2#post407821330

The weakness I see in most class-based systems that also use ability scores is that certain classes can invariably treat some ability scores as dump stats. Maybe once in a blue moon will you give a (shit) that your fighter has a 3 Charisma, but in 99.9% of circumstances, it will not negatively affect you at all.

This may sound bad, but I think it's because designers approach ability scores with realism in mind first. Using recent D&D editions as an example, they correlate ability scores with what a person realistically does, only later realizing that while everyone in the party can regularly benefit from AC, Reflex, and Initiative bonuses, most characters can be drooling buffoons, Charisma-wise, and suffer no ill game effects. You can't dump Wisdom because everyone suffers from that. You can't dump Dex because everyone suffers from that. Other stats are easier to dump.

Because different classes have different ability score needs, it produces lopsided/variable utility in the stats (e.g. see how 3E/3.5 designers had to wrestle with bonuses to Strength because even they knew that something was wrong). It also means certain build types are really only beneficial as pure roleplaying/gimmick builds. It's cool that I can RP those characters, but make no mistake: they're pretty bad in the field compared to "normal" builds. Such systems would be no worse for it if the "opt-out" weaknesses of dump stats were addressed at a fundamental level.

Editing in two more:
http://forums.obsidian.net/topic/60...characters-and-races/?view=findpost&p=1191115

Character Creation
At a minimum, players will be able to specify their main character's name, sex, class, race (including subrace), culture, traits, ability scores, portrait, and the fundamental starting options of his or her class (gear, skills, and talents).

http://forums.obsidian.net/topic/62...-character-at-age-21/?view=findpost&p=1272720

I like giving players options to play a range of character ages. Some of that can be reflected in portraits or in dialogue. I would rather not place mechanical modifications on character age. If you think an older character should be weaker and wiser, you can arrange your ability scores to reflect that.

As far as the story goes, we do not currently plan to have any restrictions on the PC's starting age (other than being an adult).

 

[Kirtai]

I wonder if this means we'll get stuff like having low charisma characters screw up social interactions by opening their big mouths at the wrong time, which the charming character has to cover for.

 

[Infinitron]

What are you trying to say, Roguey?

The weakness I see in most class-based systems that also use ability scores is that certain classes can invariably treat some ability scores as dump stats.

Well, we have classes, so let's remove ability scores then.

This may sound bad, but I think it's because designers approach ability scores with realism in mind first.

Or will Josh be able to come up with some gamist adaptation of the classical D&D ability scores? (In before Codex weeping about how they don't make sense)

 

[Roguey]

Please check out my edit. One-way-ticket to gamistville.

 

[Kem0sabe]

I wonder if this means we'll get stuff like having low charisma characters screw up social interactions by opening their big mouths at the wrong time, which the charming character has to cover for.

We can only hope, but i think most dev´s can´t be assed to write completely different dialogues trees based on INT or CH.

 

[Infinitron]

I wonder if this means we'll get stuff like having low charisma characters screw up social interactions by opening their big mouths at the wrong time, which the charming character has to cover for.

We can only hope, but i think most dev´s can´t be assed to write completely different dialogues trees based on INT or CH.

Actually, low-int "stupid" dialogue is already confirmed for Project Eternity.

 

[hiver]

You guys know anything about multiclassing or dual classes? Or any other kind of mixing classes.
I asked on formspring but didnt get an answer yet.

maybe sending a few more questions about it would help?