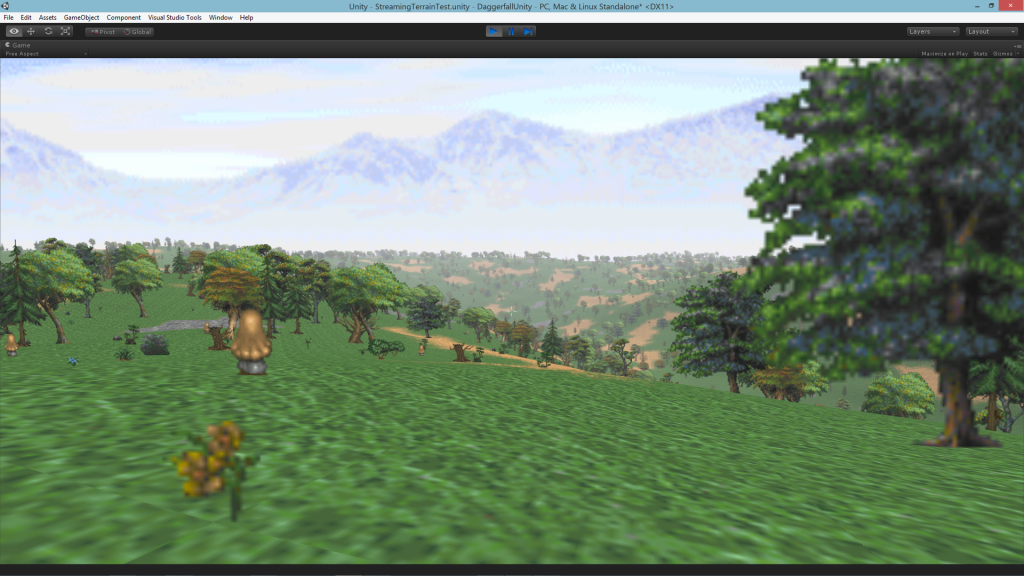
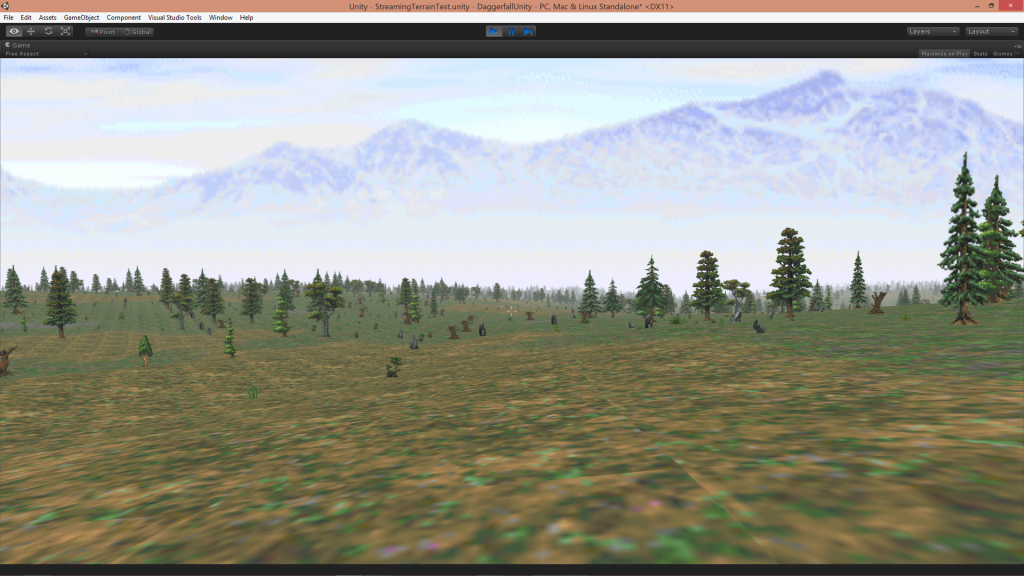
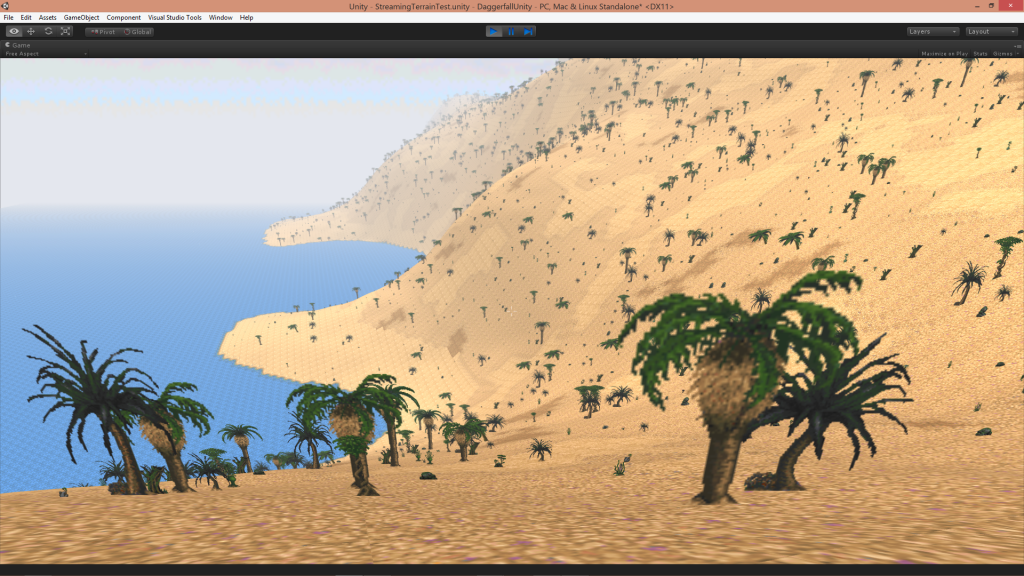
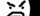It has been a long time since my last update but my life has been undergoing a series of changes – for the better – that have occupied my time. I have started to settle in and have resumed working on the DaggerXL Beta. In this post I will talk a little about the Daggerfall Renderer, starting with some simple basics.
Below is the Object structure – the structure itself (i.e. size of variables and such) is fully known though a few members still do not have appropriate names yet, u1, u2, u3. As you can see the world space position is stored in
(xPosition, yPosition, zPosition) in inches and the rotation angles are stored in
angles[3]. Positions are stored in absolute world space – this position is not relative but the actual position on the world map. The angles range from
0 – 2047 – which maps to 360 degrees. In other words
512 = 90 degrees,
2048 = 360 degrees.
struct Object
{
//0x00
byte type;
//0x01
word angles[3];
//0x07
int xPosition;
//0x0B
int yPosition;
//0x0F
int zPosition;
//0x13
word index2;
//0x15
word flags;
//0x17
word dataSize;
//0x19
word index;
//0x1B
word arrayIndex;
//0x1D
word model;
//0x1F
int ID;
//0x23
byte u1;
word u2;
byte u3;
//0x27
int curLocID;
//0x2B
dword time;
//0x2F
Object *target2;
//0x33
Object *target;
//0x37
Object *siblingNext;
//0x3B
Object *siblingPrev;
//0x3F
Object *child;
//0x43
Object *parent;
};
To generate a rotation transform for an object or for the camera Daggerfall uses the following matrix:
Given angles: x=xAngle, y=yAngle, z=zAngle – the Daggerfall rotation matrix =
[ cos(z)*cos(y) + sin(x)*sin(z)*sin(y) -sin(z)*cos(x) sin(z)*sin(x)*cos(y) ]
[-sin(x)*sin(y)*cos(z) + sin(z)*cos(y) cos(x)*cos(z) -cos(z)*sin(x)*cos(y) ]
[ sin(y)*cos(x) sin(x) cos(x)*cos(y) ]
The 3×3 rotation matrix is stored in
1.3.28 fixed point.
Here is the function used to generate the 3×3 rotation matrix from the angles:
void Build3x3Matrix(int xAngle, int yAngle, int zAngle, int *matrix)
{
int x = xAngle&0x07ff;
int y = yAngle&0x07ff;
int z = zAngle&0x07ff;
const int64 half = 134217728LL;
int64 c = (int64)sinTable[z] * (int64)sinTable[y] + half;
camAngle0 = (int)( c >> 28LL );
c = (int64)sinTable[y] * (int64)sinTable[512+z] + half;
camAngle1 = (int)( c >> 28LL );
c = (int64)sinTable[x] * (int64)sinTable[512+y] + half;
camAngle2 = (int)( c >> 28LL );
c = (int64)sinTable[512+z] * (int64)sinTable[512+y] +
(int64)sinTable[x] * (int64)camAngle0 + half;
matrix[0] = (int)( c >> 28LL );
c = -(int64)sinTable[z] * (int64)sinTable[x+512] + half;
matrix[1] = (int)( c >> 28LL );
c = (int64)sinTable[z] * (int64)camAngle2 + half;
matrix[2] = (int)( c >> 28LL ) - camAngle1;
c = -(int64)sinTable[x] * (int64)camAngle1 +
(int64)sinTable[z] * (int64)sinTable[y+512] + half;
matrix[3] = (int)( c >> 28LL );
c = (int64)sinTable[x+512] * (int64)sinTable[z+512] + half;
matrix[4] = (int)( c >> 28LL );
c = -(int64)sinTable[z+512] * camAngle2;
matrix[5] = (int)( c >> 28LL ) - camAngle0;
c = (int64)sinTable[y] * (int64)sinTable[x+512] + half;
matrix[6] = (int)( c >> 28LL );
matrix[7] = sinTable[x];
c = (int64)sinTable[x+512] * (int64)sinTable[y+512] + half;
matrix[8] = (int)( c >> 28LL );
}
A few things to note – the fixed point format is
1.3.28 so 64 bit math is required to avoid overflows, fortunately x86 assembly makes this fairly easy to do quickly. Also note that Daggerfall has a sine table that stores the sin values for all angles ranging from
0 to 2047 (remember that this maps to 0 to 360 degrees). As you can see the cosine values are computed as
sinTable[angle+512] – since sine and cosine are out of phase by 90 degrees, we can compute cosine as
cos(angle) = sin(angle+90degrees) which Daggerfall does to limit the size of the table.
The camera uses the same position and angles to generate the view and projection matrices. However the way positions are transformed into screenspace are a little different from most modern engines. The projection matrix is build directly from the view matrix by scaling by the x relative and y relative screen aspect ratios, built as follows:
void BuildAspectScaledMatrix(int *rotMatrix, int *outScaledMatrix)
{
int64 c = (int64)rotMatrix[0] * (int64)screenAspectX;
outScaledMatrix[0] = (int)( c >> 14LL );
c = (int64)rotMatrix[1] * (int64)screenAspectX;
outScaledMatrix[1] = (int)( c >> 14LL );
c = (int64)rotMatrix[2] * (int64)screenAspectX;
outScaledMatrix[2] = (int)( c >> 14LL );
c = (int64)rotMatrix[3] * (int64)screenAspectY;
outScaledMatrix[3] = (int)( c >> 14LL );
c = (int64)rotMatrix[4] * (int64)screenAspectY;
outScaledMatrix[4] = (int)( c >> 14LL );
c = (int64)rotMatrix[5] * (int64)screenAspectY;
outScaledMatrix[5] = (int)( c >> 14LL );
outScaledMatrix[6] = rotMatrix[6];
outScaledMatrix[7] = rotMatrix[7];
outScaledMatrix[8] = rotMatrix[8];
}
Note that the
screenAspectX and
screenAspectY are stored in
1.17.14 fixed point but the resulting projection matrix is still stored in
1.3.28 fixed point.
Positions in view space are stored as 1.23.8 fixed point so a position can be transformed as follows:
Given (x,y,z) in absolute world space:
(Note
s_xPosition, s_yPosition and s_zPosition are the camera positions extracted from the camera objects and used by the renderer).
//Convert to camera relative coordinates, stored in 1.23.8 fixed point), still in inches.
int viewX = (x - s_xPosition)*256;
int viewY = (y - s_yPosition)*256;
int viewZ = (z - s_zPosition)*256;
TransformPoint(&viewX, &viewY, &viewZ, projMatrix);
void TransformPoint(int *x, int *y, int *z, int *matrix)
{
int64 xp = (int64)(*x)*16LL;
int64 yp = (int64)(*y)*16LL;
int64 zp = (int64)(*z)*16LL;
*x = (int)( ( xp*(int64)matrix[0] + yp*(int64)matrix[1] + zp*(int64)matrix[2] ) >> 32LL );
*y = (int)( ( xp*(int64)matrix[3] + yp*(int64)matrix[4] + zp*(int64)matrix[5] ) >> 32LL );
*z = (int)( ( xp*(int64)matrix[6] + yp*(int64)matrix[7] + zp*(int64)matrix[8] ) >> 32LL );
}
Finally the following functions are used to cull the bounds, stored as spheres – center in relative camera coordinates and radius in inches.
enum ClipPlanes_e
{
PLANE_NEGX = 1,
PLANE_POSX = 2,
PLANE_POSY = 4,
PLANE_NEGY = 8,
PLANE_NEAR = 16,
PLANE_FAR = 32,
PLANES_ALL = PLANE_NEGX | PLANE_POSX | PLANE_POSY | PLANE_NEGY | PLANE_NEAR | PLANE_FAR
};
static int nearPlane=2560; //[1E9CC0] :the near plane is 10 inches.
static int farPlane =393216; //[1E9CC4] :the far plane is 128 feet
//(at normal maximum settings).
int CullPlaneDistX(int xScaled, int yScaled, int radius)
{
int r = (zRadius*xScaled)>>16 + (xRadius*yScaled)>>16;
if ( r < 0 )
{
r = -r;
}
return r+radius;
}
int CullPlaneDistY(int xScaled, int yScaled, int radius)
{
int r = (zRadius*xScaled)>>16 + (yRadius*yScaled)>>16;
if ( r < 0 )
{
r = -r;
}
return r+radius;
}
//Is the sphere: center = (x,y,z), radius = r at least partially visible?
//Returns 0 if visible else 1.
//Note that the sphere position must be relative to the camera and be in 1.23.8 fixed point format.
int IsSphereVisible(int x, int y, int z, int r)
{
//transform into projection space.
TransformPoint(&x, &y, &z, projMatrix);
//figure out which planes the sphere needs to be tested against.
int clipFlags = PLANES_ALL; //6 planes = 111111 binary = 63
if ( z >= nearPlane )
{
clipFlags ^= PLANE_NEAR;
}
if ( z <= farPlane )
{
clipFlags ^= PLANE_FAR;
}
if ( x >= -z )
{
clipFlags ^= PLANE_NEGX;
}
if ( x <= z )
{
clipFlags ^= PLANE_POSX;
}
if ( y <= z )
{
clipFlags ^= PLANE_POSY;
}
if ( y >= -z )
{
clipFlags ^= PLANE_NEGY;
}
//compute plane data.
xRadius = (int)( ((int64)x*(int64)x*(int64)ScreenAspectA )>>32LL );
yRadius = (int)( ((int64)y*(int64)y*(int64)ScreenAspectA_SC)>>32LL );
zRadius = z;
//test against each plane based on the clipflags set (see above).
if ( clipFlags )
{
if ( s_clipFlags&PLANE_NEAR )
{
if ( z+r <= nearPlane )
return 1;
}
if ( s_clipFlags&PLANE_FAR )
{
if ( z-r >= farPlane )
return 1;
}
if ( s_clipFlags&PLANE_NEGX )
{
if ( CullPlaneDistX(ScreenX_Scaled, ScreenH_Scaled, r) <= 0 )
return 1;
}
if ( s_clipFlags&PLANE_POSX )
{
if ( CullPlaneDistX(ScreenX_Scaled, -ScreenH_Scaled, r) <= 0 )
return 1;
}
if ( s_clipFlags&PLANE_POSY )
{
if ( CullPlaneDistY(varD34, -varD30, r) <= 0 )
return 1;
}
if ( s_clipFlags&PLANE_NEGY )
{
if ( CullPlaneDistY(varD34, varD30, r) <= 0 )
return 1;
}
}
return 0;
}
Anyway that is enough about the renderer for this post but I will talk about the lighting system, more about culling objects and other topics in future blog posts. If you want to see the original assembly for these functions, visit the
Renderer Part I – Original Functions in Assembly page. As you will see I have rearranged the code a little to make some things more clear.



















![Glory to Codexia! [2012] Codex 2012](/forums/smiles/campaign_tags/campaign_slushfund2012.png)